题目内容
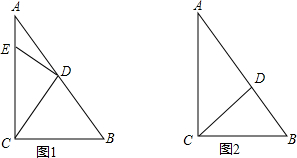
5.在正方形ABCD中,CD=5,BD是一条对角线,动点E在直线CD上运动(不与点C,D不重合),连接AE,平移△ADE,使点D移动到点C,得到△BCF,过点F作FG⊥BD于点G,连接AG,EG.(1)如图①,当点E在直线CD上时,线段EF的长为5(直接填空).
(2)如图②,当点E在线段CD的延长线上时,求证:△AGD≌△EGF;
(3)点E在直线CD上运动过程中,当线段DE的长为5$\sqrt{3}$时,直接写出∠AGF的度数,不必说明理由.

分析 (1)根据DE=CF,可以推出EF=CD,由此即可解决问题.
(2)欲证明△AGD≌△EGF,只要证明∠ADG=∠EFG=45°,DG=FG,AD=EF即可.
(3)∠AGF的度数为60°或120°,分两种情形见图③④,分别求解即可.
解答 (1)解:如图①中,∵△BCF是由△ADE平移所得,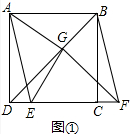
∴DE=CF,
∴EF=CD=5,
故答案为5.
(2)证明:∵四边形ABCD是正方形,
∴CD=AD=EF,∠ADG=∠FDG=45°,
∵FG⊥BD,
∴∠DFG=∠FDG=45°,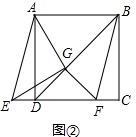
∴DG=GF,
在△AGD和△EGF中,
$\left\{\begin{array}{l}{AD=EF}\\{∠ADG=∠GFE}\\{DG=FG}\end{array}\right.$,
∴△AGD≌△EGF.
(3)∠AGF的度数为60°或120°.
理由;如图③中,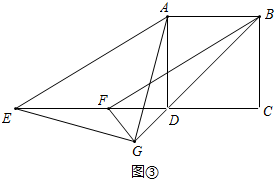 在RT△AED中,∵∠ADE=90°,ED=5$\sqrt{3}$,AD=5,
在RT△AED中,∵∠ADE=90°,ED=5$\sqrt{3}$,AD=5,
∴tan∠AED=$\frac{AD}{ED}$=$\frac{\sqrt{3}}{3}$,
∴∠AED=30°,由(2)可知△AGD≌△EGF,
∴∠EGF=∠AGD,EG=AG,
∴∠EGA=∠FCD=90°,∠GEA=∠EAG=45°,
∴∠DEG=15°,
∵∠DFG=∠FEG+∠FGE,
∴∠EGF=∠AGD=30°,
∴∠AGF=90°-∠AGD=60°,
如图④中,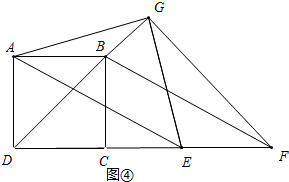 同理可证∠AGD=∠EGF=30°,可得∠AGF=∠AGD+∠DGF=120°.
同理可证∠AGD=∠EGF=30°,可得∠AGF=∠AGD+∠DGF=120°.
∴∠AGF的度数为60°或120°.
点评 本题考查正方形的性质、全等三角形的判定和性质、等腰直角三角形的性质和判定等知识,解题的关键是正确寻找全等三角形,寻找特殊三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
15.不等式$\left\{\begin{array}{l}{-x<3}\\{4x-8≤12}\end{array}\right.$的解集是( )
| A. | -3<x≤5 | B. | 3<x≤5 | C. | 3<x≤-5 | D. | -3<x<5 |
20.下列关于“-1”的说法中,错误的是( )
| A. | -1的相反数是1 | B. | -1是最小的负整数 | ||
| C. | -1的绝对值是1 | D. | -1是最大的负整数 |
10.已知第1组数据:1,3,5,7的方差为S12,第2组数据:52,54,56,58的方差为S22,第3组数据:2016,2015,2014,2013的方差为S32,则S12,S22,S32的大小关系是( )
| A. | S32>S22>S12 | B. | S12=S22<S32 | C. | S12=S22>S32 | D. | S12=S22=S32 |
17.下面的图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14. 如图,一只小猴顺着一根斜放的竹竿往上爬,眼睛一直盯着挂在上端的帽子,在小猴爬行的过程中,视线与水平方向所成角( )
如图,一只小猴顺着一根斜放的竹竿往上爬,眼睛一直盯着挂在上端的帽子,在小猴爬行的过程中,视线与水平方向所成角( )
 如图,一只小猴顺着一根斜放的竹竿往上爬,眼睛一直盯着挂在上端的帽子,在小猴爬行的过程中,视线与水平方向所成角( )
如图,一只小猴顺着一根斜放的竹竿往上爬,眼睛一直盯着挂在上端的帽子,在小猴爬行的过程中,视线与水平方向所成角( )| A. | 逐渐变大 | B. | 逐渐变小 | C. | 不变 | D. | 无法确定 |
15.下面的图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
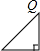
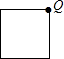
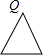
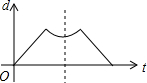 设圆、等腰直角三角形、正方形和等腰三角形边界上的一个定点为Q(如四个选项中的图形),动点P从点Q出发,在其边界上按顺时针方向匀速运动一周后又回到起点Q.设点P运动的时间是t,点P和点Q之间的距离是d,如图是d与t之间函数关系的大致图象,则该图形可能是( )
设圆、等腰直角三角形、正方形和等腰三角形边界上的一个定点为Q(如四个选项中的图形),动点P从点Q出发,在其边界上按顺时针方向匀速运动一周后又回到起点Q.设点P运动的时间是t,点P和点Q之间的距离是d,如图是d与t之间函数关系的大致图象,则该图形可能是( )