题目内容
16.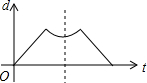 设圆、等腰直角三角形、正方形和等腰三角形边界上的一个定点为Q(如四个选项中的图形),动点P从点Q出发,在其边界上按顺时针方向匀速运动一周后又回到起点Q.设点P运动的时间是t,点P和点Q之间的距离是d,如图是d与t之间函数关系的大致图象,则该图形可能是( )
设圆、等腰直角三角形、正方形和等腰三角形边界上的一个定点为Q(如四个选项中的图形),动点P从点Q出发,在其边界上按顺时针方向匀速运动一周后又回到起点Q.设点P运动的时间是t,点P和点Q之间的距离是d,如图是d与t之间函数关系的大致图象,则该图形可能是( )| A. |  | B. | 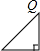 | C. | 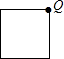 | D. | 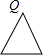 |
分析 根据圆,等腰直角三角形,正方形,等边三角形性质,分析得到d随t的增大而变化关系,然后选择答案即可.
解答 解:A、圆,随着点P运动,d的长度先变速增加至PQ为直径,然后再变速减小至点P回到点Q,题干图象不符合;
B、等腰直角三角形,点P在一开始沿直角边运动时,d的长度为直线变化增大,
沿另一条直角边运动时,设直角边长为a,则d=$\sqrt{{a}^{2}+(t-a)^{2}}$(a<t<2a),
在斜边运动时,d的长度为直线变化减小,且长度与直角边不相等,题干图象不符合;
C、正方形,点P在开始与结束的两边上直线变化,在另两边上,先变速增加至∠Q的对角顶点,再变速减小至另一顶点,题干图象不符合;
D、等边三角形,点P在开始与结束的两边上直线变化,
在点Q的对边上时,设等边三角形的边长为a,
则y=$\sqrt{(\frac{\sqrt{3}}{2}a)^{2}+(\frac{3}{2}a-t)^{2}}$(a<x<2a),符合题干图象;
故选:D.
点评 本题考查了动点问题函数图象,熟练掌握圆,等腰直角三角形,正方形以及等边三角形的性质,理清点P在各边时d的长度的变化情况是解题的关键.

练习册系列答案
相关题目
6.我们知道:31=3,32=9,33=27,34=81,35=243…;81=8,82=64,83=512,84=4096,85=32768…,那么1282015+632016结果的个位数字是( )
| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
4.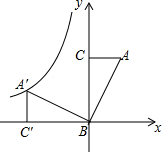 如图,Rt△ABC的一个顶点B在原点,BC在y轴上,直角边AC=1,BC=2,把Rt△ABC绕点B逆时针旋转90°,顶点A的对应点为A′.若反比例函数y=$\frac{m}{x}$的图象经过点A′,则m的值为( )
如图,Rt△ABC的一个顶点B在原点,BC在y轴上,直角边AC=1,BC=2,把Rt△ABC绕点B逆时针旋转90°,顶点A的对应点为A′.若反比例函数y=$\frac{m}{x}$的图象经过点A′,则m的值为( )
 如图,Rt△ABC的一个顶点B在原点,BC在y轴上,直角边AC=1,BC=2,把Rt△ABC绕点B逆时针旋转90°,顶点A的对应点为A′.若反比例函数y=$\frac{m}{x}$的图象经过点A′,则m的值为( )
如图,Rt△ABC的一个顶点B在原点,BC在y轴上,直角边AC=1,BC=2,把Rt△ABC绕点B逆时针旋转90°,顶点A的对应点为A′.若反比例函数y=$\frac{m}{x}$的图象经过点A′,则m的值为( )| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
11.关于x的一元二次方程x2-4sinα•x+2=0有两个等根,则锐角α的度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
8.为了建设节约型社会,鼓励居民节约用水,志愿小组在社区宣传时,随机对该社区10户居民的月用水量进行了调查,下表是这10户居民2016年4月份用水量的调查结果:
则这10户居民用水量的中位数为( )
| 居民户数 | 1 | 5 | 3 | 1 |
| 月用水量(米3/户) | 10 | 15 | 20 | 25 |
| A. | 15 | B. | 17.5 | C. | 20 | D. | 20 |
6.圆锥的底面半径为4,母线长为10,则该圆锥的侧面积为( )
| A. | 80π | B. | 40π | C. | 20π | D. | 10π |
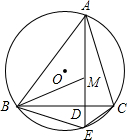 如图,点M是△ABC的内心,AM的延长线交边BC于点D,交△ABC外接圆⊙O于点E,连接BE、CE.
如图,点M是△ABC的内心,AM的延长线交边BC于点D,交△ABC外接圆⊙O于点E,连接BE、CE.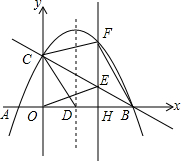 如图,抛物线y=-$\frac{1}{2}$x2+mx+2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴直线x=$\frac{3}{2}$交x轴于点D.
如图,抛物线y=-$\frac{1}{2}$x2+mx+2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴直线x=$\frac{3}{2}$交x轴于点D.