题目内容
2.某商场购进一批单价为16元的日用品,销售一段时间后,经调查发现,每月销售数量y(件)与售出价格x(元/件)满足关系y=-30x+90.(1)若某月卖出该日用品210件,求商品售出价格为每件多少元?
(2)为了获得最大的利润,商品售出价格应定为每件多少元?此时的最大利润是多少元?
分析 (1)将y=210代入解析式,求得x的值即可;
(2)根据“总利润=单件利润×销售量”列出函数解析式,再配方成顶点式结合二次函数性质可得答案.
解答 解:(1)∵某月卖出该日用品210件
∴210=-30x+960,
∴x=25,
∴商品售出价格为每件25元.
(2)设利润为W元
W=(x-16)(-30x+960),
=30(-x+32)(x-16)
=30(-x2+48x-512)
=-30(x-24)2+1920,
∵a=-30<0,
∴当x=24时,P有最大值,最大值为1920.
∴为了获得最大的利润,商品售出价格应定为每件24元.
点评 本题主要考查二次函数的应用,理解题意一找到题目蕴含的相等关系是解题的关键.

练习册系列答案
相关题目
13. 如图,点D,E分别在△ABC 的AB,AC边上,且DE∥BC,如果AD:AB=2:3,那么DE:BC等于( )
如图,点D,E分别在△ABC 的AB,AC边上,且DE∥BC,如果AD:AB=2:3,那么DE:BC等于( )
 如图,点D,E分别在△ABC 的AB,AC边上,且DE∥BC,如果AD:AB=2:3,那么DE:BC等于( )
如图,点D,E分别在△ABC 的AB,AC边上,且DE∥BC,如果AD:AB=2:3,那么DE:BC等于( )| A. | 3:2 | B. | 2:5 | C. | 2:3 | D. | 3:5 |
17.下列计算正确的是( )
| A. | 4a-9a=5a | B. | a-a=a | C. | 4a+a=5 | D. | a+a=2a |
 如图,几何体是由3个大小完全一样的正方体组成的,它的主视图是( )
如图,几何体是由3个大小完全一样的正方体组成的,它的主视图是( )



 如图所示,已知△ABC中,AD是∠BAC的平分线,E为AD上一点,EF⊥BC于F,∠B=40°,∠C=70°,则∠DEF=15°.
如图所示,已知△ABC中,AD是∠BAC的平分线,E为AD上一点,EF⊥BC于F,∠B=40°,∠C=70°,则∠DEF=15°.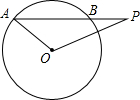 如图,已知⊙O的半径为5cm,弦AB长为8cm,P是AB延长线上一点,BP=2cm,则OP=3$\sqrt{5}$cm.
如图,已知⊙O的半径为5cm,弦AB长为8cm,P是AB延长线上一点,BP=2cm,则OP=3$\sqrt{5}$cm.