题目内容
1.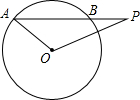 如图,已知⊙O的半径为5cm,弦AB长为8cm,P是AB延长线上一点,BP=2cm,则OP=3$\sqrt{5}$cm.
如图,已知⊙O的半径为5cm,弦AB长为8cm,P是AB延长线上一点,BP=2cm,则OP=3$\sqrt{5}$cm.
分析 过O作OC⊥AB于C,根据垂径定理求出AC、BC,根据勾股定理求出OC,根据勾股定理求出OP即可.
解答 解:过O作OC⊥AB于C,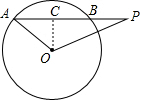
则∠OCP=∠ACO=90°,
∵OC⊥AB,OC过O,
∴AC=BC=$\frac{1}{2}$AB=$\frac{1}{2}$×8cm=4cm,
∵BP=2cm,
∴PC=BC+BP=6cm,
在Rt△ACO中,由勾股定理得:OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3(cm),
在Rt△PCO中,由勾股定理得:OP=$\sqrt{P{C}^{2}+O{C}^{2}}$=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$(cm),
故答案为:$3\sqrt{5}$.
点评 本题考查了勾股定理和垂径定理的应用,能灵活运用垂径定理进行推理是解此题的关键,注意:垂直于弦的直径平分弦.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
1.同时抛掷两枚质量均匀的硬币,恰好一枚正面朝上、一枚反面朝上的概率是( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
19.在平面直角坐标系中,若点P坐标为(2,-3),则它位于第几象限( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.根据下面的两种移动电话计费方式表,考虑下列问题.
(1)一个月内在本地通话200分和350分,按方式一需交费多少元?按方式二呢?
(2)对于某个本地通话时间,通话时间多少分钟时会出现按两种计费方式收费一样多?(此问列方程解)
| 方式一 | 方式二 | |
| 月租费 | 30元/月 | 0元 |
| 本地的通话费 | 0.30元/分 | 0.40元/分 |
(2)对于某个本地通话时间,通话时间多少分钟时会出现按两种计费方式收费一样多?(此问列方程解)
13.某中学为了解七年级学生的视力情况,从560名七年级学生中随机抽取了50名学生进行视力检查,那么这次抽样检查中,样本容量是( )
| A. | 560 | B. | 50 | ||
| C. | 被抽取的50名学生 | D. | 七年级的560名学生 |
10.在Rt△ABC中,∠C=90°,C为斜边,a,b为直角边,a+b=14,c=10,则Rt△ABC面积为( )
| A. | 24 | B. | 36 | C. | 48 | D. | 60 |
11. 如图,下列条件中,能判定AB∥CD的是( )
如图,下列条件中,能判定AB∥CD的是( )
 如图,下列条件中,能判定AB∥CD的是( )
如图,下列条件中,能判定AB∥CD的是( )| A. | ∠1=∠2 | B. | ∠4=∠6 | C. | ∠4=∠5 | D. | ∠1+∠3=180° |