题目内容
10．
如图，几何体是由3个大小完全一样的正方体组成的，它的主视图是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 根据主视图是从正面看得到的图形，可得答案．
解答 解：从正面看第一层是两个小正方形，第二层右边一个小正方形，
故选：B．
点评 本题考查了简单组合体的三视图，从正面看得到的图形是主视图．
练习册系列答案
阅读快车系列答案
相关题目
1．同时抛掷两枚质量均匀的硬币，恰好一枚正面朝上、一枚反面朝上的概率是（ ）
| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
18．
有这样一个问题：探究函数y=$\frac{{\sqrt{x+2}}}{x}$的图象与性质．小美根据学习函数的经验，对函数y=$\frac{{\sqrt{x+2}}}{x}$的图象与性质进行了探究．下面是小美的探究过程，请补充完整：
（1）函数y=$\frac{{\sqrt{x+2}}}{x}$的自变量x的取值范围是x≥-2且x≠0；
（2）下表是y与x的几组对应值．
求m的值；
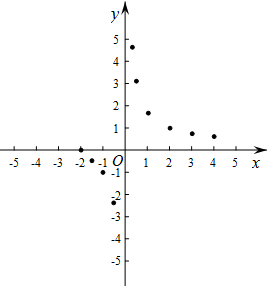
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的一条性质：当-2≤x＜0或x＞0时，y随x增大而减小．
有这样一个问题：探究函数y=$\frac{{\sqrt{x+2}}}{x}$的图象与性质．小美根据学习函数的经验，对函数y=$\frac{{\sqrt{x+2}}}{x}$的图象与性质进行了探究．下面是小美的探究过程，请补充完整：（1）函数y=$\frac{{\sqrt{x+2}}}{x}$的自变量x的取值范围是x≥-2且x≠0；
（2）下表是y与x的几组对应值．
| x | -2 | -$\frac{3}{2}$ | -1 | -$\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | 0 | -$\frac{{\sqrt{2}}}{3}$ | -1 | -$\sqrt{6}$ | $\sqrt{21}$ | $\sqrt{10}$ | $\sqrt{3}$ | m | $\frac{{\sqrt{5}}}{3}$ | $\frac{{\sqrt{6}}}{4}$ | … |
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的一条性质：当-2≤x＜0或x＞0时，y随x增大而减小．
如图，△ACB和△ADE均为等边三角形，点C、E、D在同一直线上，连接BD．
15．-$\frac{3}{2}$的倒数是（ ）
| A． | -$\frac{3}{2}$ | B． | -$\frac{2}{3}$ | C． | $\frac{3}{2}$ | D． | $\frac{2}{3}$ |
19．在平面直角坐标系中，若点P坐标为（2，-3），则它位于第几象限（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
10．在Rt△ABC中，∠C=90°，C为斜边，a，b为直角边，a+b=14，c=10，则Rt△ABC面积为（ ）
| A． | 24 | B． | 36 | C． | 48 | D． | 60 |