题目内容
7．解方程：（1）x2-x+$\frac{1}{4}$=0
（2）（x+3）2=（1-2x）2．
分析 （1）因式分解法求解可得；
（2）直接开平方法求解可得．
解答 解：（1）∵x2-x+$\frac{1}{4}$=0，
∴（x-$\frac{1}{2}$）2=0，
∴x=$\frac{1}{2}$；
（2）∵（x+3）2=（1-2x）2，
∴x+3=1-2x或x+3=2x-1，
解得：x=-$\frac{2}{3}$或x=4．
点评 本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．
练习册系列答案
相关题目
18．
有这样一个问题：探究函数y=$\frac{{\sqrt{x+2}}}{x}$的图象与性质．小美根据学习函数的经验，对函数y=$\frac{{\sqrt{x+2}}}{x}$的图象与性质进行了探究．下面是小美的探究过程，请补充完整：
（1）函数y=$\frac{{\sqrt{x+2}}}{x}$的自变量x的取值范围是x≥-2且x≠0；
（2）下表是y与x的几组对应值．
求m的值；
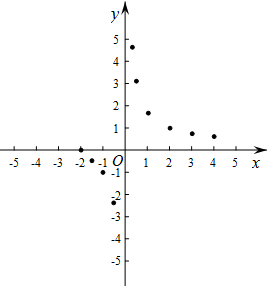
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的一条性质：当-2≤x＜0或x＞0时，y随x增大而减小．
有这样一个问题：探究函数y=$\frac{{\sqrt{x+2}}}{x}$的图象与性质．小美根据学习函数的经验，对函数y=$\frac{{\sqrt{x+2}}}{x}$的图象与性质进行了探究．下面是小美的探究过程，请补充完整：（1）函数y=$\frac{{\sqrt{x+2}}}{x}$的自变量x的取值范围是x≥-2且x≠0；
（2）下表是y与x的几组对应值．
| x | -2 | -$\frac{3}{2}$ | -1 | -$\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | 0 | -$\frac{{\sqrt{2}}}{3}$ | -1 | -$\sqrt{6}$ | $\sqrt{21}$ | $\sqrt{10}$ | $\sqrt{3}$ | m | $\frac{{\sqrt{5}}}{3}$ | $\frac{{\sqrt{6}}}{4}$ | … |
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的一条性质：当-2≤x＜0或x＞0时，y随x增大而减小．
15．-$\frac{3}{2}$的倒数是（ ）
| A． | -$\frac{3}{2}$ | B． | -$\frac{2}{3}$ | C． | $\frac{3}{2}$ | D． | $\frac{2}{3}$ |
19．在平面直角坐标系中，若点P坐标为（2，-3），则它位于第几象限（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
6．根据下面的两种移动电话计费方式表，考虑下列问题．
（1）一个月内在本地通话200分和350分，按方式一需交费多少元？按方式二呢？
（2）对于某个本地通话时间，通话时间多少分钟时会出现按两种计费方式收费一样多？（此问列方程解）
| 方式一 | 方式二 | |
| 月租费 | 30元/月 | 0元 |
| 本地的通话费 | 0.30元/分 | 0.40元/分 |
（2）对于某个本地通话时间，通话时间多少分钟时会出现按两种计费方式收费一样多？（此问列方程解）