题目内容
8.已知关于x的一元二次方程x2-2x-t+1=0有两个实数根.(1)求t的取值范围;
(2)设v是方程的一个实数根,且满足(v2-2v+3)(t-3)=-5,求t的值.
分析 (1)根据一元二次方程有两个实数根即△≥0,可得关于t的不等式,解不等式可得;
(2)根据方程的解得v2-2v=t-1,整体代入可得关于t的方程,解方程可得.
解答 解:(1)∵关于x的一元二次方程x2-2x-t+1=0有两个实数根,
∴△≥0,即△=4-4(-t+1)≥0,
∴t≥0;
(2)∵v是方程的一个实数根,
∴把x=v代入方程得:v2-2v-t+1=0,即v2-2v=t-1,
∵(v2-2v+3)(t-3)=-5,
∴(t-1+3)(t-3)=-5,
∴(t+2)(t-3)=-5,整理得:t2-t-1=0,
∴解得此方程的根为:t=$\frac{1±\sqrt{5}}{2}$,
又∵t≥0,
∴t=$\frac{1+\sqrt{5}}{2}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
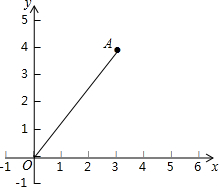 在直角坐标系中,O为坐标原点,已知A(3,4),在x轴上确定一点P,使△OAP为等腰三角形,求符合条件的点P的坐标.
在直角坐标系中,O为坐标原点,已知A(3,4),在x轴上确定一点P,使△OAP为等腰三角形,求符合条件的点P的坐标.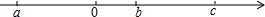 实数a,b,c在数轴上的位置如图所示.
实数a,b,c在数轴上的位置如图所示.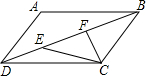 如图,在?ABCD中,∠ADB=2∠BDC,点E为对角线BD上一点,CF垂直平分线段BE,连接EC.求证:DE=BC.
如图,在?ABCD中,∠ADB=2∠BDC,点E为对角线BD上一点,CF垂直平分线段BE,连接EC.求证:DE=BC.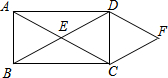 已知:如图,在矩形ABCD中,对角线BD与AC相交于点E,DF∥AC,CF∥BD,直线DF与CF相交于点F.求证:四边形EDFC是菱形.
已知:如图,在矩形ABCD中,对角线BD与AC相交于点E,DF∥AC,CF∥BD,直线DF与CF相交于点F.求证:四边形EDFC是菱形.