题目内容
如图，在正方形ABCD的边AB上任取一点E（A、B两点除外），过E、B、C三点的圆与BD相交于点F．求证：EF⊥FC且EF=FC．考点：正方形的性质,圆周角定理
专题：证明题
分析：连结EC，根据正方形的性质和圆周角定理可得CE是圆的直径，从而得到EF⊥FC，再根据∠FEC=45°，根据等腰直角三角形的性质即可得到EF=FC，从而得证．
解答：
证明：连结EC，
∵四边形ABCD是正方形，
∴∠EBC=90°，
∴CE是圆的直径，
∴∠EFC=90°，
∵BD是正方形ABCD的对角线，
∴∠DBC=45°，
∴∠FEC=45°，
∴△EFC是等腰直角三角形，
∴EF=FC．
故EF⊥FC且EF=FC．
证明：连结EC，∵四边形ABCD是正方形，
∴∠EBC=90°，
∴CE是圆的直径，
∴∠EFC=90°，
∵BD是正方形ABCD的对角线，
∴∠DBC=45°，
∴∠FEC=45°，
∴△EFC是等腰直角三角形，
∴EF=FC．
故EF⊥FC且EF=FC．
点评：考查了正方形的性质和圆周角定理，本题关键是证明△EFC是等腰直角三角形．
练习册系列答案
阅读快车系列答案
相关题目
若一次函数y=（1-2k）x-k的函数值y随x的增大而增大，且此函数的图象不经过第二象限，则k的取值范围是（ ）
A、k＜
| ||
| B、k≥0 | ||
C、0≤k＜
| ||
D、k≤0或k＞
|
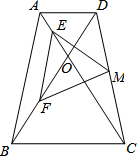如图，在等腰梯形ABCD中，AD∥BC（BC＞AD），对角线AC、BD交于点O，∠BOC=60°且E、F分别为OA、OB的中点，M为CD的中点，求证：△EFM是等边三角形．
如图，反比例函数y=