题目内容
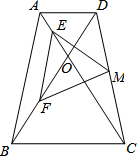 如图,在等腰梯形ABCD中,AD∥BC(BC>AD),对角线AC、BD交于点O,∠BOC=60°且E、F分别为OA、OB的中点,M为CD的中点,求证:△EFM是等边三角形.
如图,在等腰梯形ABCD中,AD∥BC(BC>AD),对角线AC、BD交于点O,∠BOC=60°且E、F分别为OA、OB的中点,M为CD的中点,求证:△EFM是等边三角形.考点:等腰梯形的性质,等边三角形的判定,三角形中位线定理
专题:证明题
分析:连接DE、CF,如图,先根据等腰梯形的性质得AB=DC,OA=OD,OB=OC,再由∠BOC=60°可判断△OBC和△OAD都为等边三角形,则根据等腰三角形的性质由
E、F分别为OA、OB的中点得到DE⊥OA,CF⊥OB,接着根据直角三角形斜边上的中线等于斜边的一半得到EM=
CD,FM=
CD;然后利用三角形中位线性质得到EF=
AB=
CD,所以EF=EM=FM,于是可判断△EFM为等边三角形.
E、F分别为OA、OB的中点得到DE⊥OA,CF⊥OB,接着根据直角三角形斜边上的中线等于斜边的一半得到EM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: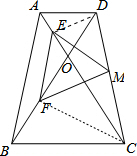 证明:连接DE、CF,如图,
证明:连接DE、CF,如图,
∵在等腰梯形ABCD中,AD∥BC(BC>AD),
∴AB=DC,OA=OD,OB=OC,
∵∠BOC=60°,
∴△OBC和△OAD都为等边三角形,
∵E、F分别为OA、OB的中点,
∴DE⊥OA,CF⊥OB,
在Rt△CDE中,∵点M为斜边CD的中点,
∴EM=
CD,
同理可得FM=
CD,
∵E、F分别为OA、OB的中点,
∴EF为△OAB的中位线,
∴EF=
AB,
∴EF=
CD,
∴EF=EM=FM,
∴△EFM为等边三角形.
 证明:连接DE、CF,如图,
证明:连接DE、CF,如图,∵在等腰梯形ABCD中,AD∥BC(BC>AD),
∴AB=DC,OA=OD,OB=OC,
∵∠BOC=60°,
∴△OBC和△OAD都为等边三角形,
∵E、F分别为OA、OB的中点,
∴DE⊥OA,CF⊥OB,
在Rt△CDE中,∵点M为斜边CD的中点,
∴EM=
| 1 |
| 2 |
同理可得FM=
| 1 |
| 2 |
∵E、F分别为OA、OB的中点,
∴EF为△OAB的中位线,
∴EF=
| 1 |
| 2 |
∴EF=
| 1 |
| 2 |
∴EF=EM=FM,
∴△EFM为等边三角形.
点评:本题考查了等腰梯形的性质:等腰梯形是轴对称图形,它的对称轴是经过上下底的中点的直线;等腰梯形同一底上的两个角相等;等腰梯形的两条对角线相等.也考查了等边三角形的判定与性质、三角形中位线性质和直角三角形斜边上的中线性质.

练习册系列答案
相关题目
根据下列条件列出的代数式,错误的是( )
| A、a、b两数的平方差为a2-b2 |
| B、a与b两数差的平方为(a-b)2 |
| C、a与b的平方的差为a2-b2 |
| D、a与b的差的平方为(a-b)2 |
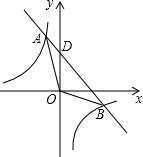 反比例函数y=-
反比例函数y=- 如图1,点A、B分别在数轴原点O的左右两侧,且
如图1,点A、B分别在数轴原点O的左右两侧,且 如图,在正方形ABCD的边AB上任取一点E(A、B两点除外),过E、B、C三点的圆与BD相交于点F.求证:EF⊥FC且EF=FC.
如图,在正方形ABCD的边AB上任取一点E(A、B两点除外),过E、B、C三点的圆与BD相交于点F.求证:EF⊥FC且EF=FC. 如图在梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,在线段AB上是否存在一点P,使得△PAD与△PBC相似?若不存在,说明理由;若存在,说出这样的点P有几个?并求出PA长?
如图在梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,在线段AB上是否存在一点P,使得△PAD与△PBC相似?若不存在,说明理由;若存在,说出这样的点P有几个?并求出PA长?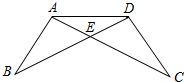 一次数学课上,老师在黑板上画了如图图形,并写下了四个等式:
一次数学课上,老师在黑板上画了如图图形,并写下了四个等式: 如图,已知AD∥BC,∠B=30°,DB平分∠ADE,求∠DEC的度数.
如图,已知AD∥BC,∠B=30°,DB平分∠ADE,求∠DEC的度数.