题目内容
 如图,A、B分别是x轴上位于原点左、右两侧的点.P(3,m),m>0,直线PA交y轴于点C(0,2),S△AOP=9.
如图,A、B分别是x轴上位于原点左、右两侧的点.P(3,m),m>0,直线PA交y轴于点C(0,2),S△AOP=9.(1)求点A的坐标及m的值;
(2)若S△BOP=S△DOP,求直线BD的解析式;
(3)在(2)的情况下,已知存在点E,使以点A、B、P、E顶点的四边形是平行四边形,请直接写出点E的坐标.
考点:一次函数综合题
专题:综合题
分析:(1)求得△AOC的面积,即可求得A的坐标,利用待定系数法即可求得AC的解析式,把x=3代入解析式即可求得m的值;
(2)设直线BD的解析式为y=ax+c(a≠0),再把P(3,3)代入得出3a+c=3,故可得出D(0,c),B(-
,0),再根据三角形的面积公式即可得出结论;
(3)如图所示,使以点A、B、P、E顶点的四边形是平行四边形的点E位置有三个,分别求出坐标即可.
(2)设直线BD的解析式为y=ax+c(a≠0),再把P(3,3)代入得出3a+c=3,故可得出D(0,c),B(-
| c |
| a |
(3)如图所示,使以点A、B、P、E顶点的四边形是平行四边形的点E位置有三个,分别求出坐标即可.
解答: 解:(1)∴S△AOC=S△AOP-S△COP=9-3=6,
解:(1)∴S△AOC=S△AOP-S△COP=9-3=6,
∴S△AOC=
OA•OC=6,即
×OA×2=6,
∴OA=6,
∴A的坐标是(-6,0),
设直线AP的解析式是y=kx+b,
将A与C坐标代入得:
,
解得:
,
∴直线的解析式是y=
x+2,
当x=3时,y=3,即m=3;
(2)设直线BD的解析式为y=ax+c(a≠0),
∵P(3,3),
∴3a+c=3,
∴D(0,c),B(-
,0),
∵S△BOP=S△DOP,
∴
OD•3=
OB•3,即c=-
,
解得:a=-1,
∴c=6,
∴BD的解析式是:y=-x+6;
(3)如图所示,E有三个位置,
∵A(-6,0),B(6,0),P(3,3),
∴PE1=PE2=AB=12,
∴E1(15,3),E2(-9,3),
由题意得:E3与E2关于点A对称,
∴E3(-3,-3),
则使以点A、B、P、E顶点的四边形是平行四边形的点E坐标为(15,3)或(-9,3)或(-3,-3).
 解:(1)∴S△AOC=S△AOP-S△COP=9-3=6,
解:(1)∴S△AOC=S△AOP-S△COP=9-3=6,∴S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴OA=6,
∴A的坐标是(-6,0),
设直线AP的解析式是y=kx+b,
将A与C坐标代入得:
|
解得:
|
∴直线的解析式是y=
| 1 |
| 3 |
当x=3时,y=3,即m=3;
(2)设直线BD的解析式为y=ax+c(a≠0),
∵P(3,3),
∴3a+c=3,
∴D(0,c),B(-
| c |
| a |
∵S△BOP=S△DOP,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| c |
| a |
解得:a=-1,
∴c=6,
∴BD的解析式是:y=-x+6;
(3)如图所示,E有三个位置,
∵A(-6,0),B(6,0),P(3,3),
∴PE1=PE2=AB=12,
∴E1(15,3),E2(-9,3),
由题意得:E3与E2关于点A对称,
∴E3(-3,-3),
则使以点A、B、P、E顶点的四边形是平行四边形的点E坐标为(15,3)或(-9,3)或(-3,-3).
点评:此题属于一次函数综合题,涉及的知识有:待定系数法确定一次函数解析式,一次函数与坐标轴的交点,坐标与图形性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
若一次函数y=(1-2k)x-k的函数值y随x的增大而增大,且此函数的图象不经过第二象限,则k的取值范围是( )
A、k<
| ||
| B、k≥0 | ||
C、0≤k<
| ||
D、k≤0或k>
|
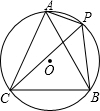 如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°,
如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°,