Question

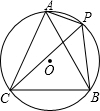如图，A、P、B、C是⊙O上的四点，∠APC=∠CPB=60°，
（1）判断△ABC的形状并证明你的结论．
（2）若⊙O的半径为4cm，求△ABC的面积．

Answer 1

考点：圆周角定理,等边三角形的判定与性质

专题：

分析：（1）直接根据圆周角定理即可得出结论．
（2）连接AO并延长交BC于点D，连接OC，由等边三角形的性质可知AD⊥BC，∠OCD=30°，故可得出OD的长，根据三角形的面积公式即可得出结论．

解答：解：（1）∵A、P、B、C是⊙O上的四点，∠APC=∠CPB=60°，
∴∠ABC=∠APC=60°，∠CAB=∠CPB=60°，
∴△ABC是等边三角形；

（2）连接AO并延长交BC于点D，连接OC，
∵△ABC是等边三角形，
∴AD⊥BC，∠OCD=30°，
∴OD=

1

2

OC=2cm，CD=OC•cos30°=4×

3

2

=2

3

cm，
∴AD=4+2=6（cm），BC=2CD=4

3

cm，
∴S_△ABC=

1

2

BC•AD=

1

2

×4

3

×6=12

3

（cm²）．

点评：本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等是解答此题的关键．