题目内容
14.解方程(1)$\frac{6}{x+6}=\frac{1}{x}$
(2)$\frac{3}{x}$+$\frac{3}{x-1}$=$\frac{x+2}{{x}^{2}-x}$.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:6x=x+6,
解得:x=$\frac{6}{5}$,
经检验x=$\frac{6}{5}$是分式方程的解;
(2)去分母得:3x-3+3x=x+2,
解得:x=1,
经检验x=1是增根,原分式方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列条件中,不能判定△ABC为直角三角形的是( )
| A. | ∠A+∠B=90° | B. | a2+b2=c2 | C. | a:b:c=3:4:5 | D. | ∠A:∠B:∠c=3:4:5 |
19.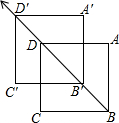 如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )
如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )
 如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )
如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )| A. | 25 | B. | 39 | C. | 47 | D. | 49 |
4.已知一弹簧称所挂重物质量x(g)与弹簧长度y(cm)之间的关系如下表:
(1)请写出弹簧长度y(cm)与所挂物体重量x(g)之间的关系式.
(2)当所挂重物质量为4.5g时,弹簧长度是多少厘米?
| x(g) | 2 | 3 | 4 | 5 | 6 | 7 | … |
| y(cm) | 8.2 | 8.3 | 8.4 | 8.5 | 8.6 | 8.7 | … |
(2)当所挂重物质量为4.5g时,弹簧长度是多少厘米?