题目内容
5.下列条件中,不能判定△ABC为直角三角形的是( )| A. | ∠A+∠B=90° | B. | a2+b2=c2 | C. | a:b:c=3:4:5 | D. | ∠A:∠B:∠c=3:4:5 |
分析 根据两锐角互余的三角形是直角三角形可得A能判定△ABC为直角三角形;根据勾股定理逆定理可得B、C能判定△ABC为直角三角形;利用三角形内角和定理计算出∠C的度数,可得D不能判定△ABC为直角三角形.
解答 解:A、∠A+∠B=90°,能判定△ABC为直角三角形,故此选项不合题意;
B、a2+b2=c2,能判定△ABC为直角三角形,故此选项不合题意;
C、32+42=52,因此a:b:c=3:4:5能判定△ABC为直角三角形,故此选项不合题意;
D、∠A:∠B:∠C=3:4:5,∠C=180°×$\frac{5}{12}$=75°,不是直角三角形,故此选项符合题意;
故选:D.
点评 此题主要考查了直角三角形的判定,关键是掌握如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
16.下列命题中错误的是( )
| A. | 对角线相等的四边形是矩形 | |
| B. | 两组对边分别相等的四边形是平行四边形 | |
| C. | 矩形的对角线相等 | |
| D. | 平行四边形的对边相等 |
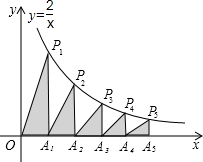 如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5=1,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5并设其面积分别为S1、S2、S3、S4、S5,则S1+S2+S3+S4+S5的值为$\frac{137}{60}$.
如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5=1,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5并设其面积分别为S1、S2、S3、S4、S5,则S1+S2+S3+S4+S5的值为$\frac{137}{60}$.