题目内容
8.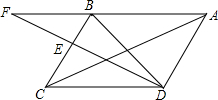 已知:如图,在菱形ABCD中,E为边BC的中点,DE与对角线AC交于点F,若∠BAC=∠EDC且EF=1,DF=2,则AC的长为2.
已知:如图,在菱形ABCD中,E为边BC的中点,DE与对角线AC交于点F,若∠BAC=∠EDC且EF=1,DF=2,则AC的长为2.
分析 先由菱形对边平行得出内错角相等∠F=∠EDC,∠BAC=∠ACD,再由已知条件证德∠F=BAC,∠EDC=∠ACD,得出AG=FG,CG=DG,即可得出AC=DF.
解答 解:如图所示: ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠F=∠EDC,∠BAC=∠ACD,
∵∠BAC=∠EDC,
∴∠F=BAC,∠EDC=∠ACD,
∴AG=FG,CG=DG,
∴AG+CG=FG+DG,
即AC=DF=2.
故答案为:2.
点评 本题考查了菱形的性质以及等腰三角形的判定与性质;证明三角形是等腰三角形是解决问题的关键.

练习册系列答案
相关题目
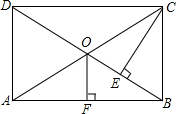 如图,矩形ABCD的对角线AC、BD相交于点O,CE⊥BD,且DE:EB=3:1,OF⊥AB于F,OF=3,求矩形对角线的长.
如图,矩形ABCD的对角线AC、BD相交于点O,CE⊥BD,且DE:EB=3:1,OF⊥AB于F,OF=3,求矩形对角线的长.
 如图,抛物线y=ax2+1,y=ax2-1(a<0)的图象与直线x=-2,x=2所围成的阴影部分图形的面积是8.
如图,抛物线y=ax2+1,y=ax2-1(a<0)的图象与直线x=-2,x=2所围成的阴影部分图形的面积是8.