题目内容
17.如图,在平面直角坐标系中,点A(-2,0),以OA为边,在第三象限内作等腰直角三角形OAC,点F是斜边AC的中点.动点M(0,n),连接MF,以MF为边作正方形FMNQ,(字母按逆时针排序).(1)求Q点坐标.(用n表示)
(2)动点N的轨迹是直线,求这条直线的解析式;
(3)连接FN,设△AMN的面积为s,求s与n的函数解析式,并写出n的取值范围.
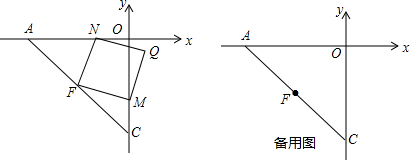
分析 (1)根据中点坐标公式得到F点的坐标,根据等腰直角三角形和正方形的性质可得N点坐标,找到点F与点M之间的关系,再根据正方形的性质即可得到Q点坐标;
(2)由于动点N的纵坐标为0,依此即可得到这条直线的解析式;
(3)根据三角形面积公式即可得到s与n的函数解析式.
解答 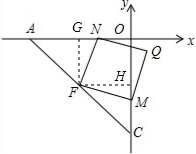 解:(1)过F作FG⊥x轴,FH⊥y轴,
解:(1)过F作FG⊥x轴,FH⊥y轴,
∵点A(-2,0),以OA为边,在第三象限内作等腰直角三角形OAC,点F是斜边AC的中点,
∴点A(0,-2),
∴点F(-1,-1);
∵四边形FMNQ是正方形,动点M(0,n),
∴MH=NG,
∴N点坐标为(-n-2,0),
∴G点坐标为(-n-1,n+1);
(2)∵动点N的坐标为(-n-2,0),
∴这条直线的解析式为y=0;
(3)△AMN的面积s=$\frac{1}{2}$AN•OM=$\frac{1}{2}$|-n-2+2|•|n|=$\frac{1}{2}$n2(n为任何实数).
点评 考查了一次函数综合题,涉及的知识点有:中点坐标公式,等腰直角三角形和正方形的性质,直线的解析式,三角形面积公式,综合性较强,作出辅助线是解题的关键,难度中等.

练习册系列答案
相关题目
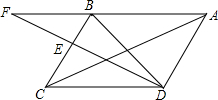 已知:如图,在菱形ABCD中,E为边BC的中点,DE与对角线AC交于点F,若∠BAC=∠EDC且EF=1,DF=2,则AC的长为2.
已知:如图,在菱形ABCD中,E为边BC的中点,DE与对角线AC交于点F,若∠BAC=∠EDC且EF=1,DF=2,则AC的长为2.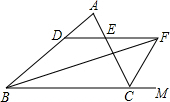 如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F,过点F作DF∥BC,交AB于点D,交AC于点E.问:
如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F,过点F作DF∥BC,交AB于点D,交AC于点E.问: