题目内容
18.抛物线y=1-x2与y轴交于点A,经过点B(0,-1)作y轴的垂线交上述抛物线于点C,D,点T是线段CD上一点,横坐标为t,连接AT交x轴于点N,点M是上述抛物线上一动点(M不与点A重合且在CD的上方),其横坐标为m,延长MN至点G,使NM=NG.(1)用m,t表示点G 的坐标;(图1供参考)
(2)设以点T为顶点的另一条抛物线恰好经过点G,M,且点M到CD的距离HM=0.25,说明点G是否在抛物线y=1-x2上,并求MT的长度.(图2供参考)
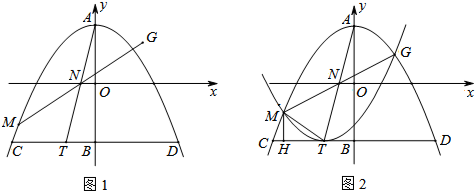
分析 (1)过点M作ME⊥x轴于E,过点G作GF⊥x轴于F,过点T作TH⊥x轴于H,求出ME=m2-1,根据△ENM≌△FNG得出GF=ME=m2-1,证出△TNH≌△ANO,HN=ON,得出点N的坐标为($\frac{1}{2}$t,0),EN=FN=$\frac{1}{2}$t-m,求出OF=t-m,即可得出点G 的坐标;
(2)设另一条抛物线的解析式为y=a(x-t)2-1,根据抛物线过点M得出抛物线解析式为y=$\frac{2-{m}^{2}}{(m-t)^{2}}$•(x-t)2-1,根据x=t-m时,y=m2-1,得出点G在抛物线上,根据MH=0.25,得出m2-1=0.75,求出点M、点G的坐标,根据点G是在抛物线y=1-x2上,得出$\frac{3}{4}$=1-(t+$\frac{\sqrt{7}}{2}$)2,求出t,再求出TH=$\frac{1}{2}$,最后根据MH=$\sqrt{M{H}^{2}+T{H}^{2}}$代入计算即可.
解答  解:(1)如图1,过点M作ME⊥x轴于E,过点G作GF⊥x轴于F,过点T作TH⊥x轴于H,
解:(1)如图1,过点M作ME⊥x轴于E,过点G作GF⊥x轴于F,过点T作TH⊥x轴于H,
∵点M的坐标是(m,1-m2),
∴ME=m2-1,
在△ENM和△FNG中,
$\left\{\begin{array}{l}{∠MNE=∠GNF}\\{∠MEN=∠GFN}\\{MN=GN}\end{array}\right.$,
∴△ENM≌△FNG(AAS),
∴GF=ME=m2-1,
∵点T的坐标为(t,1),点A的坐标为(0,1),
∴TH=AO,
在△TNH和△ANO中,
$\left\{\begin{array}{l}{∠ANO=∠TNH}\\{∠AON=∠THN}\\{TH=AO}\end{array}\right.$,
∴△TNH≌△ANO,
∴HN=ON,
∴点N的坐标为($\frac{1}{2}$t,0),
∴EN=$\frac{1}{2}$t-m,
∴FN=$\frac{1}{2}$t-m,
∴OF=$\frac{1}{2}$t-m+$\frac{1}{2}$t=t-m,
∴点G 的坐标(t-m,m2-1);
(2)如图2,设另一条抛物线的解析式为y=a(x-t)2-1,
∵抛物线过点M,
∴1-m2=a(m-t)2-1,
∴a=$\frac{2-{m}^{2}}{(m-t)^{2}}$,
∴抛物线解析式为:y=$\frac{2-{m}^{2}}{(m-t)^{2}}$•(x-t)2-1,
∵当x=t-m时,
y=$\frac{2-{m}^{2}}{(m-t)^{2}}$•(t-m-t)2-1=m2-1,
∴点G在抛物线上,
∵MH=0.25,
∴MH=1-0.25=0.75,
∴m2-1=0.75,
∴m1=$\frac{\sqrt{7}}{2}$(舍去),m2=-$\frac{\sqrt{7}}{2}$,
∴点M的坐标为(-$\frac{\sqrt{7}}{2}$,-$\frac{3}{4}$),
点G的坐标为(t+$\frac{\sqrt{7}}{2}$,$\frac{3}{4}$),
∵点G是在抛物线y=1-x2上,
∴$\frac{3}{4}$=1-(t+$\frac{\sqrt{7}}{2}$)2,
t1=$\frac{1-\sqrt{7}}{2}$,t2=$\frac{-1-\sqrt{7}}{2}$(舍去)
∴TH=t-m=$\frac{1-\sqrt{7}}{2}$-(-$\frac{\sqrt{7}}{2}$)=$\frac{1}{2}$,
∴MH=$\sqrt{M{H}^{2}+T{H}^{2}}$=$\sqrt{(\frac{1}{4})^{2}+({\frac{1}{2})}^{2}}$=$\frac{\sqrt{5}}{4}$.
点评 此题考查了二次函数的综合,用到的知识点是二次函数的图象与性质、勾股定理、全等三角形的判定与性质等,关键是根据题意作出辅助线,注意把不合题意的解舍去.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第2014次“移位”后,则他所处顶点的编号是3.
如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第2014次“移位”后,则他所处顶点的编号是3.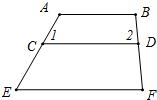 如图,下列六个条件:①∠1=∠E;②∠2=∠F;③∠A+∠1=180°;④∠B+∠2=180°;⑤∠DCE+∠E=180°;⑥∠CDF+∠F=180°,从中选取两个条件作为题设,使得命题“如果∠1=∠E,∠B+∠2=180°,那么AB∥EF”是一个真命题,并证明你的结论.
如图,下列六个条件:①∠1=∠E;②∠2=∠F;③∠A+∠1=180°;④∠B+∠2=180°;⑤∠DCE+∠E=180°;⑥∠CDF+∠F=180°,从中选取两个条件作为题设,使得命题“如果∠1=∠E,∠B+∠2=180°,那么AB∥EF”是一个真命题,并证明你的结论.
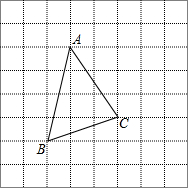 如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,用一个最小的圆去覆盖△ABC,请你在如图所示的网格中,用直尺画出该圆的圆心(保留作图痕迹),并简要说明画图的方法(不要求证明)填什么.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,用一个最小的圆去覆盖△ABC,请你在如图所示的网格中,用直尺画出该圆的圆心(保留作图痕迹),并简要说明画图的方法(不要求证明)填什么.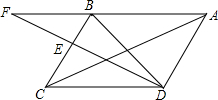 已知:如图,在菱形ABCD中,E为边BC的中点,DE与对角线AC交于点F,若∠BAC=∠EDC且EF=1,DF=2,则AC的长为2.
已知:如图,在菱形ABCD中,E为边BC的中点,DE与对角线AC交于点F,若∠BAC=∠EDC且EF=1,DF=2,则AC的长为2.