题目内容
1.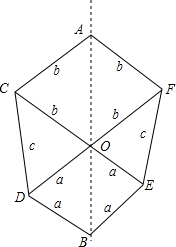 (1)制作如图①的纸片,并沿对称轴AB把它剪开;
(1)制作如图①的纸片,并沿对称轴AB把它剪开;(2)把对称轴AB一侧的部分,沿AB翻折,再绕AB的中点旋转180°,画出翻折、旋转后的图②;
(3)试利用①,②验证勾股定理.
分析 (2)沿AB翻折后的图形是图形①的一半,取AB的中点,根据中心对称的性质画出图形即可;
(3)分别求出图①和图②的面积,由两个图形的面积相等,即可得出结论.
解答 (2)解:如图所示 :
:
(3)证明:由①得:S①=a2+b2+2×$\frac{1}{2}$ab=a2+b2+ab,
由②得:S②=c2+2×$\frac{1}{2}$ab=c2+ab,
∴a2+b2+ab=c2+ab,
∴a2+b2=c2.
点评 本题考查了翻折的性质、中心对称的性质以及作图、正方形和直角三角形面积的计算、勾股定理的证明;熟练掌握翻折和中心对称的性质,画出图形是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.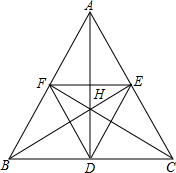 如图,锐角△ABC的垂心为H,三条高的垂足分为D、E、F,则H是△DEF的( )
如图,锐角△ABC的垂心为H,三条高的垂足分为D、E、F,则H是△DEF的( )
 如图,锐角△ABC的垂心为H,三条高的垂足分为D、E、F,则H是△DEF的( )
如图,锐角△ABC的垂心为H,三条高的垂足分为D、E、F,则H是△DEF的( )| A. | 垂心 | B. | 重心 | C. | 内心 | D. | 外心 |
11. 如图,CD是⊙O的直径且CD=4,CD⊥AB于点E,∠A=30°,则弦AB的长为( )
如图,CD是⊙O的直径且CD=4,CD⊥AB于点E,∠A=30°,则弦AB的长为( )
 如图,CD是⊙O的直径且CD=4,CD⊥AB于点E,∠A=30°,则弦AB的长为( )
如图,CD是⊙O的直径且CD=4,CD⊥AB于点E,∠A=30°,则弦AB的长为( )| A. | 1 | B. | 2 | C. | $2\sqrt{3}$ | D. | $4\sqrt{3}$ |
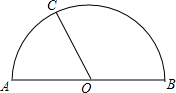 如图,在以AB为直径的半圆中,半径OC=4,且S扇形AOC:S扇形BOC=3:5.
如图,在以AB为直径的半圆中,半径OC=4,且S扇形AOC:S扇形BOC=3:5. 如图,?ABCD中,AE平分∠DAB,∠B=100°,则∠DAE等于40°.
如图,?ABCD中,AE平分∠DAB,∠B=100°,则∠DAE等于40°.