题目内容
13.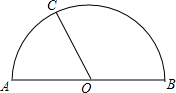 如图,在以AB为直径的半圆中,半径OC=4,且S扇形AOC:S扇形BOC=3:5.
如图,在以AB为直径的半圆中,半径OC=4,且S扇形AOC:S扇形BOC=3:5.(1)求扇形BOC的面积;
(2)在半圆内作另一条半径OD,若S扇形COD:S扇形BOC=3:10,求扇形AOD面积.
分析 (1)由已知条件得到∠AOC:∠BOC=3:5,求得∠BOC=112.5°,即可得到结论;
(2)①当D在$\widehat{AC}$上时,有已知条件得到S扇形AOC=2S扇形COD=S扇形AOD+S扇形COD,于是得到S扇形AOD=S扇形COD=$\frac{1}{2}$S扇形AOC,求得S扇形AOC=8π-5π=3π,即可得到结论,②当D在$\widehat{BC}$上时,根据已知条件得到S扇形COD=$\frac{3}{10}$S扇形BOC=$\frac{3}{2}$π,于是得到结论.
解答 解:(1)∵S扇形AOC:S扇形BOC=3:5,
∴∠AOC:∠BOC=3:5,
∵∠AOC+∠BOC=180°,
∴∠BOC=112.5°,
∴扇形BOC的面积=$\frac{112.5•π•{4}^{2}}{360}$=5π;
(2)①当D在$\widehat{AC}$上时,
∵S扇形COD:S扇形BOC=3:10,S扇形AOC:S扇形BOC=3:5=6:10,
∴S扇形AOC=2S扇形COD=S扇形AOD+S扇形COD,
∴S扇形AOD=S扇形COD=$\frac{1}{2}$S扇形AOC,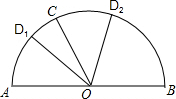
由(1)求得扇形BOC的面积=5π,
∴S扇形AOC=8π-5π=3π,
∴扇形AOD面积=$\frac{3}{2}$π,
②当D在$\widehat{BC}$上时,∵S扇形COD:S扇形BOC=3:10,
∴S扇形COD=$\frac{3}{10}$S扇形BOC=$\frac{3}{2}$π,
∴S扇形AOD=S扇形AOC+S扇形COD=3$π+\frac{3}{2}π$=$\frac{9}{2}$π.
点评 本题考查了扇形的面积的计算,熟记扇形的面积公式是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
8.如图,是一个几何体的三视图,则这几何体的表面积是( )
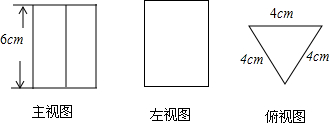

| A. | 72cm2 | B. | 60cm2 | C. | (72+4$\sqrt{3}$)cm2 | D. | (72+8$\sqrt{3}$)cm2 |
5.若x2-2x-3=0,则2x2-4x+5的值为( )
| A. | 6 | B. | 5 | C. | -1 | D. | 11 |
3.下列方程中,是关于x的一元二次方程的是( )
| A. | 3(x+1)2=2(x+1) | B. | $\frac{1}{x^2}+\frac{1}{x}-2=0$ | C. | ax2+bx+c=0 | D. | 2x=1 |
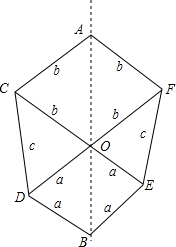 (1)制作如图①的纸片,并沿对称轴AB把它剪开;
(1)制作如图①的纸片,并沿对称轴AB把它剪开;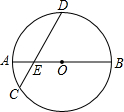 如图,⊙O的直径AB和弦CD相交于点E,∠DEB=45°.
如图,⊙O的直径AB和弦CD相交于点E,∠DEB=45°. 如图,已知AE是△ABC的角平分线,∠B=66°,∠C=42°.求∠AEB的度数.
如图,已知AE是△ABC的角平分线,∠B=66°,∠C=42°.求∠AEB的度数.