题目内容
19．
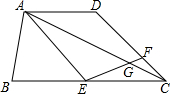四边形ABCD中，AD∥BC，AD=$\frac{1}{2}$BC，E为BC的中点，F在DC上，且CF=$\frac{1}{3}$DC，连AC交EF于点G．（1）求证：△AGE∽△CGF；
（2）若AC=10，求CG的长．
分析 （1）只要证明AD=CE，AD∥CE，推出四边形ADCE是平行四边形即可解决问题；
（2）由AE∥CF，推出$\frac{CF}{AE}$=$\frac{CG}{AG}$，根据AE=CD，CF=$\frac{1}{3}$CD即可推出CG：AG=1：3，由此即可解决问题；
解答 （1）证明：∵BC=2AD，BE=CE，
∴AD=EC，∵AD∥EC，
∴四边形ADCE是平行四边形，
∴AE∥CD，
∴△AGE∽△CGF．
（2）解：∵AE∥CF，
∴$\frac{CF}{AE}$=$\frac{CG}{AG}$，
∵四边形ADCE是平行四边形，
∴AE=CD，
∵CF=$\frac{1}{3}$CD，
∴$\frac{CG}{AG}$=$\frac{1}{3}$，
∵AC=10，
∴CG=$\frac{1}{4}$×10=$\frac{5}{2}$．
点评 本题考查相似三角形的判定和性质、平行四边形的判定和性质、平行线分线段成比例定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
练习册系列答案
相关题目
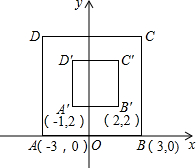如图，在平面直角坐标xOy中，对正方形ABCD及其内部的每个点进行如下操作：把每一个点的横，纵坐标都乘以同一个实数a，将得到的点先向右平移m个单位，再向上平移n个单位（m＞0，n＞0），得到正方形A′B′C′D′及其内部的点，其中点A、B的对应点分别为A′、B′．已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合，则点F的坐标为（1，4）．
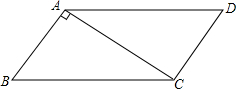如图：在?ABCD中，CA⊥BA，AB=3，AC=4，求?ABCD的周长及面积．
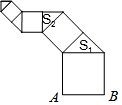按如图所示的方式作正方形和等腰直角三角形，若第一个正方形的边AB=1，第1个等腰直角三角形面积为S1，第2个等腰直角三角形的面积为S2，…，第n个等腰直角三角形的面积为Sn（其中n为正整数），则Sn=$\frac{1}{{2}^{n+1}}$．
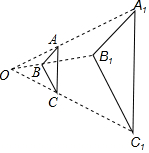如图，△ABC与△A1B1C1是以点O为位似中心的位似图形，且位似比为1：3，若△A1B1C1面积为3，则△ABC的面积为$\frac{1}{3}$．
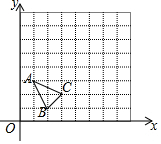如图，△ABC的三个顶点均在格点上，且A（1，3），B（2，1）