题目内容
14．已知等腰三角形的一边长是9cm，另一边长是5cm，那么这个等腰三角形的周长是（ ）| A． | 19cm | B． | 23cm | C． | 16cm | D． | 19cm或23cm |
分析 题目给出等腰三角形有两条边长为5cm和9cm，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．
解答 解：①当腰是5cm时，三角形的三边是：5cm，5cm，9cm，能构成三角形，
则等腰三角形的周长=5+5+9=19cm；
②当腰是9cm时，三角形的三边是：5cm，9cm，9cm，能构成三角形，
则等腰三角形的周长=5+9+9=23cm；
因此这个等腰三角形的周长为19或23cm．
故选D．
点评 本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．
练习册系列答案
发散思维新课堂系列答案
相关题目
4．
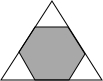如图，把边长是15cm的正三角形纸板，剪去三个小正三角形后，得到一个正六边形，则剪去的小正三角形的边长是（ ）
如图，把边长是15cm的正三角形纸板，剪去三个小正三角形后，得到一个正六边形，则剪去的小正三角形的边长是（ ）| A． | 3cm | B． | 4cm | C． | 5cm | D． | 6cm |
如图，已知在△ABC中，中线BD、CE交于点O，且△ABC的面积为60，试求四边形ADOE的面积．
2．在下列说法中，正确的是（ ）
| A． | 如果两个三角形全等，则它们必是关于直线成轴对称的图形 | |
| B． | 如果两个三角形关于某直线成轴对称，那么它们是全等三角形 | |
| C． | 等腰三角形底边中线是对称轴 | |
| D． | 一条线段是关于经过该线段中点的直线成轴对称的图形 |
如图，已知在△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线DE交AC于点E，交BC于点D，求证：BD=2DC．
19．已知$\frac{x}{2}=\frac{y}{3}=\frac{z}{5}$，则$\frac{x+3y-z}{2x-y+z}$的值是（ ）
| A． | 1 | B． | $\frac{3}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{3}{2}$ |
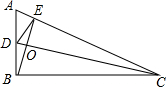如图，D、E分别是△ABC的边AB、AC上的点，BE、CD相交于点O，且AD•AB=AE•AC，△OEC与△ODB相似吗？为什么？