题目内容
3.已知抛物线经过点A(2,-2),与点B(-1,-8).在下列两种情况下,分别求抛物线的函数表达式:(1)当抛物线的顶点在y轴上时;
(2)当抛物线的顶点在x轴上时.
分析 (1)设抛物线顶点式解析式y=ax2+b,再把点A、B的坐标代入,求出a、b的值即可得解.
(2)设抛物线顶点式解析式y=a(x+h)2,再把点A、B的坐标代入,求出a、h的值即可得解
解答 解:(1)根据题意设抛物线的解析式为y=ax2+b,
∵抛物线经过点A(2,-2),与点B(-1,-8).
∴$\left\{\begin{array}{l}{4a+b=-2}\\{a+b=-8}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=-10}\end{array}\right.$,
∴抛物线的函数表达式为y=2x2-10;
(2)根据题意设抛物线的解析式为y=a(x-h)2,
∵抛物线经过点A(2,-2),与点B(-1,-8).
∴$\left\{\begin{array}{l}{a(2-h)^{2}=-2}\\{a(-1-h)^{2}=-8}\end{array}\right.$解得$\left\{\begin{array}{l}{a=-\frac{2}{9}}\\{h=5}\end{array}\right.$或$\left\{\begin{array}{l}{a=-2}\\{h=1}\end{array}\right.$,
∴抛物线的函数表达式为y=-$\frac{2}{9}$(x-5)2或y=-2(x-1)2.
点评 本题考查了待定系数法求二次函数解析式,利用顶点式解析式求解更加简便.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
14.已知等腰三角形的一边长是9cm,另一边长是5cm,那么这个等腰三角形的周长是( )
| A. | 19cm | B. | 23cm | C. | 16cm | D. | 19cm或23cm |
7.为了解我市九年级学生升学考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:40分;B:39-35分;C:34-30分;D:29-20分; E:19-0分) 统计如表.根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为32,b的值为10;
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数”.请问:甲同学的体育成绩应在B分数段内(填相应分数段的字母).
(3)若把成绩在35分以上(含35分)定为优秀,则我市今年8000名九年级学生中体育成绩为优秀的学生人数约有6400名.
| 分数段 | 人数(人) | 频率 |
| A | 48 | 0.48 |
| B | a | 0.32 |
| C | b | 0.10 |
| D | c | d |
| E | e | 0.05 |
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数”.请问:甲同学的体育成绩应在B分数段内(填相应分数段的字母).
(3)若把成绩在35分以上(含35分)定为优秀,则我市今年8000名九年级学生中体育成绩为优秀的学生人数约有6400名.
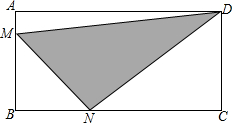 如图,矩形ABCD中,AB=6cm,BC=12cm.点M从点A开始沿AB边向点B以1cm/秒的速度向B点移动,点N从点B开始沿BC边以2cm/秒的速度向点C移动.若M,N分别从A,B点同时出发,设移动时间为t(0<t<6),△DMN的面积为S.
如图,矩形ABCD中,AB=6cm,BC=12cm.点M从点A开始沿AB边向点B以1cm/秒的速度向B点移动,点N从点B开始沿BC边以2cm/秒的速度向点C移动.若M,N分别从A,B点同时出发,设移动时间为t(0<t<6),△DMN的面积为S.