题目内容
1.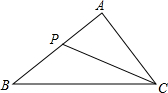 如图,点P在△ABC的边AB上,要判断△ACP∽△ABC,添加一个条件,错误的是( )
如图,点P在△ABC的边AB上,要判断△ACP∽△ABC,添加一个条件,错误的是( )| A. | ∠ACP=∠B | B. | ∠APC=∠ACB | C. | $\frac{AP}{AC}$=$\frac{AC}{AB}$ | D. | $\frac{AC}{CP}$=$\frac{AB}{BC}$ |
分析 根据两组对应边成比例,且夹角相等的两个三角形相似以及根据两个角对应相等,则两个三角形相似;再结合有两组边对应成比例的两个三角形不一定相似得出答案.
解答 解:A、∵∠ACP=∠B∠A=∠A,
∴△ACP∽△ABC,故此选项错误;
B、∵∠APC=∠ACB,∠A=∠A,
∴△ACP∽△ABC,故此选项错误;
C、∵$\frac{AP}{AC}$=$\frac{AC}{AB}$,∠A=∠A,
∴△ACP∽△ABC,故此选项错误;
D、两组边对应成比例的两个三角形不一定相似,故此选项正确.
故选D.
点评 本题考查了相似三角形的判定,熟练掌握相似三角形的判定定理是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11. 如图,矩形ABCD对角线AC,BD相交于点O,过O点作EF⊥AC,分别交AD,BC于E,F点.若△CDE的周长为10cm,则矩形ABCD的周长为( )
如图,矩形ABCD对角线AC,BD相交于点O,过O点作EF⊥AC,分别交AD,BC于E,F点.若△CDE的周长为10cm,则矩形ABCD的周长为( )
 如图,矩形ABCD对角线AC,BD相交于点O,过O点作EF⊥AC,分别交AD,BC于E,F点.若△CDE的周长为10cm,则矩形ABCD的周长为( )
如图,矩形ABCD对角线AC,BD相交于点O,过O点作EF⊥AC,分别交AD,BC于E,F点.若△CDE的周长为10cm,则矩形ABCD的周长为( )| A. | 15cm | B. | 20cm | C. | 30cm | D. | 40cm |
12. 如图所示,过直线l外一点A作l的平行线可以按以下的步骤完成:
如图所示,过直线l外一点A作l的平行线可以按以下的步骤完成:
一贴:用三角板的最长边紧贴着直线l,即使得最长边所在的直线与直线l重合;
二靠:用一个直尺紧靠着三角板的一条较短的边;
三移:按住三角板,沿着直尺移动到合适的位置,使得三角板的最长边所在的直线经过点A;
四画:沿着三角板最长边所在的直线画出一条直线,这就是经过点A和l平行的直线.这样作图依据的原理是( )
 如图所示,过直线l外一点A作l的平行线可以按以下的步骤完成:
如图所示,过直线l外一点A作l的平行线可以按以下的步骤完成:一贴:用三角板的最长边紧贴着直线l,即使得最长边所在的直线与直线l重合;
二靠:用一个直尺紧靠着三角板的一条较短的边;
三移:按住三角板,沿着直尺移动到合适的位置,使得三角板的最长边所在的直线经过点A;
四画:沿着三角板最长边所在的直线画出一条直线,这就是经过点A和l平行的直线.这样作图依据的原理是( )
| A. | 内错角相等,两直线平行 | B. | 同位角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 两直线平行,内错角相等 |
9.已知|2x+y+1|+(x+2y-7)2=0,则(x+y)2的值为( )
| A. | 0 | B. | 4 | C. | 8 | D. | 16 |
16.适合下列条件的△ABC中,直角三角形的个数为( )
①a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$;
②a=6,∠A=45°;
③∠A=32°,∠B=58°;
④a=7,b=24,c=25.
①a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$;
②a=6,∠A=45°;
③∠A=32°,∠B=58°;
④a=7,b=24,c=25.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.一直角三角形的一条直角边长是7cm,另一条直角边与斜边长的和是49cm,则斜边的长( )
| A. | 18cm | B. | 20 cm | C. | 24 cm | D. | 25cm |
13.已知圆锥的底面半径为1cm,母线长为3cm,则圆锥的侧面积是( )
| A. | 6 cm2 | B. | 3π cm2 | C. | 6π cm2 | D. | $\frac{3π}{2}$cm2 |
11.已知a<b,则下列四个不等式中,不正确的是( )
| A. | a+2<b+2 | B. | -a+2<-b+2 | C. | $\frac{1}{2}$a<$\frac{1}{2}$b | D. | 2a-1<2b-1 |