题目内容
7. 如果小球在如图所示的七巧板上自由滚动,并随机停留在这七巧板的某个位置上(不考虑停在边线的情况),那么它最终停留在四边形EFLH的概率是$\frac{1}{8}$.
如果小球在如图所示的七巧板上自由滚动,并随机停留在这七巧板的某个位置上(不考虑停在边线的情况),那么它最终停留在四边形EFLH的概率是$\frac{1}{8}$.
分析 直接利用七巧板得出各边长之间的关系,再利用四边形面积求法结合概率公式得出答案.
解答 解:由题意可得:EF=$\frac{1}{2}$DF,平行四边形EFLH的高为:$\frac{1}{4}$AF,
故四边形EFLH的面积为:$\frac{1}{8}$四边形ABDF的面积,
故最终停留在四边形EFLH的概率是:$\frac{1}{8}$.
故答案为:$\frac{1}{8}$.
点评 此题主要考查了几何概率以及七巧板,正确得出各边之间的关系是解题关键.

练习册系列答案
相关题目
18. 甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
 甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )| A. | 前2分钟,乙的平均速度比甲快 | |
| B. | 5分钟时两人都跑了500米 | |
| C. | 甲跑完800米的平均速度为100米/分 | |
| D. | 甲乙两人8分钟各跑了800米 |
2.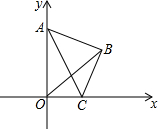 如图,在平面直角坐标系中,已知AB=BC,∠ABC=90°,若点A落在y轴上,点C落在x轴上,△ABC的形状始终不变,随着点C由原点O向x轴正半轴方向运动,点A沿y轴负半轴方向运动到终点O,在此次运动过程中,线段OB的长度变化情况是( )
如图,在平面直角坐标系中,已知AB=BC,∠ABC=90°,若点A落在y轴上,点C落在x轴上,△ABC的形状始终不变,随着点C由原点O向x轴正半轴方向运动,点A沿y轴负半轴方向运动到终点O,在此次运动过程中,线段OB的长度变化情况是( )
 如图,在平面直角坐标系中,已知AB=BC,∠ABC=90°,若点A落在y轴上,点C落在x轴上,△ABC的形状始终不变,随着点C由原点O向x轴正半轴方向运动,点A沿y轴负半轴方向运动到终点O,在此次运动过程中,线段OB的长度变化情况是( )
如图,在平面直角坐标系中,已知AB=BC,∠ABC=90°,若点A落在y轴上,点C落在x轴上,△ABC的形状始终不变,随着点C由原点O向x轴正半轴方向运动,点A沿y轴负半轴方向运动到终点O,在此次运动过程中,线段OB的长度变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先减小后增大 | D. | 先增大后减小 |
12. 如图所示,过直线l外一点A作l的平行线可以按以下的步骤完成:
如图所示,过直线l外一点A作l的平行线可以按以下的步骤完成:
一贴:用三角板的最长边紧贴着直线l,即使得最长边所在的直线与直线l重合;
二靠:用一个直尺紧靠着三角板的一条较短的边;
三移:按住三角板,沿着直尺移动到合适的位置,使得三角板的最长边所在的直线经过点A;
四画:沿着三角板最长边所在的直线画出一条直线,这就是经过点A和l平行的直线.这样作图依据的原理是( )
 如图所示,过直线l外一点A作l的平行线可以按以下的步骤完成:
如图所示,过直线l外一点A作l的平行线可以按以下的步骤完成:一贴:用三角板的最长边紧贴着直线l,即使得最长边所在的直线与直线l重合;
二靠:用一个直尺紧靠着三角板的一条较短的边;
三移:按住三角板,沿着直尺移动到合适的位置,使得三角板的最长边所在的直线经过点A;
四画:沿着三角板最长边所在的直线画出一条直线,这就是经过点A和l平行的直线.这样作图依据的原理是( )
| A. | 内错角相等,两直线平行 | B. | 同位角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 两直线平行,内错角相等 |
19.某同学使用计算器求30个数据的平均数时,错将其中的一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( )
| A. | -3.5 | B. | 3 | C. | 0.5 | D. | -3 |
 如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:①OH∥BF,②GH=$\frac{1}{4}$BC,③OD=$\frac{1}{2}$BF,④∠CHF=45°.正确结论的个数为( )
如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:①OH∥BF,②GH=$\frac{1}{4}$BC,③OD=$\frac{1}{2}$BF,④∠CHF=45°.正确结论的个数为( )
 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),将△ABC先向下平移5个单位长度,再向右平移8个单位长度得到△DEF,请画出△DEF.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),将△ABC先向下平移5个单位长度,再向右平移8个单位长度得到△DEF,请画出△DEF.