题目内容
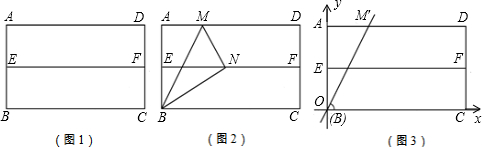
5.在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:第一步:对折矩形纸片ABCD,使AD与BC重合,把纸片展开,得到折痕EF(如图1);
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图2).
请解答以下问题:
(1)如图2,若延长MN交BC于P,△BMP是什么三角形?请证明你的结论;
(2)在图2中,若AB=a,BC=b,a、b满足什么关系,才能在矩形纸片ABCD上剪出符合(1)中结论的三角形纸片BMP?
(3)设矩形ABCD的边AB=2,BC=4,并建立如图3所示的直角坐标系.设直线BM′为y=kx,当∠M′BC=60°时,求k的值.此时,将△ABM′沿BM′折叠,点A是否落在EF上(E、F分别为AB、CD中点),为什么?
分析 (1)连接AN,可证△ABN为等边三角形,可求得∠ABM=∠NBM=30°,则可求得∠PBM=∠BMP=60°,可证得△BMP为等边三角形;
(2)由题意可知BC>BP,在Rt△BNP中,可求得a=BPcos30°,则可找到a、b满足的关系;
(3)在Rt△ABM′中可求得AM′的长,则可求得M′的坐标,代入直线y=kx可求得k的值;设△ABM′沿BM′折叠后点A在矩形OADC内的对应点为A′,过A′作A′H⊥BC于点H,在△A′BH中可求得A′H、BH的长,可求得A′点的坐标,进行判断即可.
解答 解:
(1)△BMP是等边三角形,
证明如下:如图1,连接AN,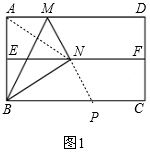
∵EF垂直平分AB,
∴AN=BN,
由折叠可知AB=BN,
∴AN=AB=BN,
∴△ABN为等边三角形,
∴∠ABN=60°,
∴∠PBN=30°,
∵∠ABM=∠NBM=30°,∠BNM=∠A=90°,
∴∠BPN=60°,∠MBP=∠MBN+∠PBN=60°,
∴∠BMP=60°,
∴∠MBP=∠BMP=∠BPM=60°,
∴△BMP为等边三角形;
(2)要在矩形纸片ABCD上剪出等边三角形BMP,则BC≥BP,
在Rt△BNP中,BN=BA=a,∠PBN=30°,
∴$\frac{a}{BP}$=cos30°,
∴BP=$\frac{a}{cos30°}$=$\frac{2\sqrt{3}}{3}$a,
∴b≥$\frac{2\sqrt{3}}{3}$a,
即当b≥$\frac{2\sqrt{3}}{3}$a时,在矩形上能剪出这样的等边三角形BMP;
(3)∵∠M′BC=60°,
∴∠ABM′=90°-60°=30°,
在Rt△ABM′中,tan∠ABM′=$\frac{AM′}{AB}$,
∴tan30°=$\frac{AM′}{2}$,解得AM′=$\frac{2\sqrt{3}}{3}$,
∴M′($\frac{2\sqrt{3}}{3}$,2),代入y=kx中,可求得k=$\sqrt{3}$;
如图2,设△ABM′沿BM′折叠后,点A落在矩形ABCD内的点为A′,过A′作A′H⊥BC于点H,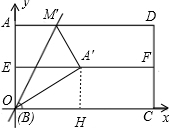
由折叠的性质可知∠A′BM′=∠ABM′=30°,A′B=AB=2,
∴∠A′BH=∠M′BH-∠A′BM′=30°,
在Rt△A′BH中,A′H=$\frac{1}{2}$A′B=1,BH=$\sqrt{3}$,
∴A′($\sqrt{3}$,1),
∴A′落在EF上.
点评 本题为一次函数的综合应用,涉及折叠的性、等边三角形的判定和性质、矩形的性质、三角函数等知识.在(1)求得∠ABM=∠NBM=30°是解题的关键,在(2)中利用三角函数的定义找到BP与a的关系是解题的关键,在(3)中求得M′和A′的坐标是解题的关键.本题考查知识点较多,综合性较强,难度适中.

| A. | x2y6 | B. | -x2y6 | C. | xy6 | D. | x2y9 |
| A. | 3.2×107 | B. | 32×105 | C. | 0.32×107 | D. | 3.2×106 |
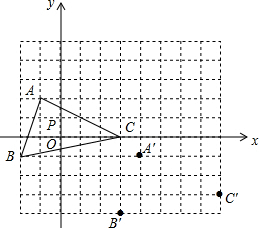 如图,△ABC中任意一点P(x0,y0)经平移后对应点为P′(x0+5,y0-3),将△ABC作同样的平移得到△A′B′C′.
如图,△ABC中任意一点P(x0,y0)经平移后对应点为P′(x0+5,y0-3),将△ABC作同样的平移得到△A′B′C′.
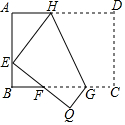 如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上的E处,EQ与BC相交于点F,若AD=8,AB=6,AE=4,则△EBF周长的大小为8.
如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上的E处,EQ与BC相交于点F,若AD=8,AB=6,AE=4,则△EBF周长的大小为8.