题目内容
20.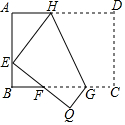 如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上的E处,EQ与BC相交于点F,若AD=8,AB=6,AE=4,则△EBF周长的大小为8.
如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上的E处,EQ与BC相交于点F,若AD=8,AB=6,AE=4,则△EBF周长的大小为8.
分析 设AH=a,则DH=AD-AH=8-a,通过勾股定理即可求出a值,再根据同角的余角互补可得出∠BFE=∠AEH,从而得出△EBF∽△HAE,根据相似三角形的周长比等于对应比即可求出结论.
解答 解:设AH=a,则DH=AD-AH=8-a,
在Rt△AEH中,∠EAH=90°,AE=4,AH=a,EH=DH=8-a,
∴EH2=AE2+AH2,即(8-a)2=42+a2,
解得:a=3.
∵∠BFE+∠BEF=90°,∠BEF+∠AEH=90°,
∴∠BFE=∠AEH.
又∵∠EAH=∠FBE=90°,
∴△EBF∽△HAE,
∴$\frac{{C}_{△EBF}}{{C}_{△HAE}}$=$\frac{BE}{AH}$=$\frac{AB-AE}{AH}$=$\frac{2}{3}$.
∵C△HAE=AE+EH+AH=AE+AD=12,
∴C△EBF=$\frac{2}{3}$C△HAE=8.
故答案为:8.
点评 本题考查了翻折变换、矩形的性质、勾股定理以及相似三角形的判定及性质,解题的关键是找出△EBF∽△HAE.本题属于中档题,难度不大,解决该题型题目时,通过勾股定理求出三角形的边长,再根据相似三角形的性质找出周长间的比例是关键.

练习册系列答案
相关题目
10.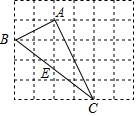 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,若点E是BC的中点,则sin∠CAE的值为( )
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,若点E是BC的中点,则sin∠CAE的值为( )
 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,若点E是BC的中点,则sin∠CAE的值为( )
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,若点E是BC的中点,则sin∠CAE的值为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
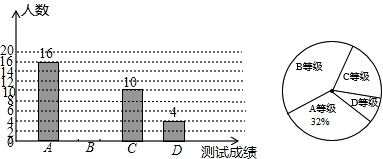
8.小明在学习了数据的收集、整理与描述后,为妈妈整理记录了10月份的家庭支出情况,并绘制成如下尚不完整的统计图表,请你根据图表信息完成下列各题:
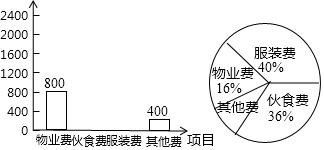
(1)10月份小明家共支出多少元?
(2)在扇形统计图中,表示“其他费”的扇形圆心角为多少度?
(3)请将表格补充完整;
(4)请将条形统计图补充完整.
| 项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
| 金额/元 | 800 | 400 |

(1)10月份小明家共支出多少元?
(2)在扇形统计图中,表示“其他费”的扇形圆心角为多少度?
(3)请将表格补充完整;
(4)请将条形统计图补充完整.
9.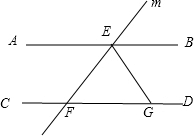 如图,已知直线AB∥CD,直线m与AB、CD相交于点E、F,EG平分∠FEB,∠EFG=50°,则∠FEG的度数为( )
如图,已知直线AB∥CD,直线m与AB、CD相交于点E、F,EG平分∠FEB,∠EFG=50°,则∠FEG的度数为( )
 如图,已知直线AB∥CD,直线m与AB、CD相交于点E、F,EG平分∠FEB,∠EFG=50°,则∠FEG的度数为( )
如图,已知直线AB∥CD,直线m与AB、CD相交于点E、F,EG平分∠FEB,∠EFG=50°,则∠FEG的度数为( )| A. | 65° | B. | 55° | C. | 45° | D. | 40° |
 抛物线L:y=a(x-x1)(x-x2)(常数a≠0)与x轴交于点A(x1,0),B(x2,0),与y轴交于点C,且x1•x2<0,AB=4,当直线l:y=-3x+t+2(常数t>0)同时经过点A,C时,t=1.
抛物线L:y=a(x-x1)(x-x2)(常数a≠0)与x轴交于点A(x1,0),B(x2,0),与y轴交于点C,且x1•x2<0,AB=4,当直线l:y=-3x+t+2(常数t>0)同时经过点A,C时,t=1.