题目内容
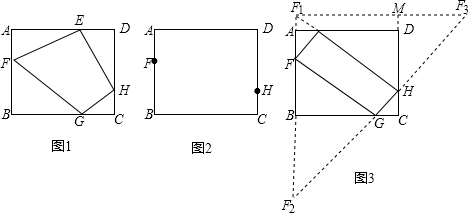
18.小敏在研究最值问题时遇到了这样的一个问题:如图1,在矩形ABCD中,AB=6,AD=8,E、F、G、H分别在矩形ABCD的边AD、AB、BC、CD上,则四边形EFGH的周长是否存在最小值?她决定按照老师讲的由特殊到一般逐步化归的思路去研究,请你帮助她完成下面的探究过程.探究1:如图2,在AF=2,DH=5的条件下,请在图2中画出周长最小的四边形EFGH,并求出周长的最小值;
探究2:在探究1的启发下,小敏画出了图3:作F关于AD的对称点F1,作F关于BC的对称点F2,作F1关于CD的对称点F3,连接F2F3交CD于H,交BC于点G,连接F1H交AD于E,连接EF、FG,借助图3,他发现四边形EFGH的周长有最小值,并顺利解决了遇到的这个问题.请求出四边形EFGH的周长的最小值.
拓广探究:解决了上述问题后,小敏又想到了新的问题,当四边形EFGH的周长最小时,四边形EFGH的面积是否存在最大值?请帮助小敏解决这个问题,若存在,请求出此时面积的最大值,若不存在请说明理由.
分析 探究1:如图1中,作F关于AD的对称点F′,F关于BC的对称点F″,连接HF′交AD于E,连接HF″交BC于G,作HM⊥AB于M.此时四边形EFGH的周长最小,最小值=EF+EH+GF+GH=EF′+EH+HG+GF″=HF′+HF″;
探究2:由题意可知四边形EFGH的周长的最小值=HF1+HF2,易知HF1是Rt△F1F2F3的斜边的中线,可得HF1=HF2=HF3,在Rt△F1F2F3中,F1F2=16,F1F3=12,
易知F2F3=$\sqrt{1{2}^{2}+1{6}^{2}}$=20,由此即可解决问题;
拓广探究:如图2中,当四边形EFGH的周长最小时,四边形EFGH是平行四边形,易知:CH:CG:GH=3:4:5,设HC=3x,GC=4x,GH=5x,则DH=6-3x,BG=8-4x,
DE=$\frac{4}{3}$(6-3x),AE=8-$\frac{4}{3}$(6-3x),BF=$\frac{3}{4}$(8-4x),AF=6-$\frac{3}{4}$(8-4x),构建二次函数即可解决问题;
解答 解:探究1:如图1中,作F关于AD的对称点F′,F关于BC的对称点F″,连接HF′交AD于E,连接HF″交BC于G,作HM⊥AB于M.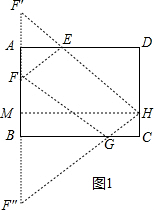
此时四边形EFGH的周长最小,最小值=EF+EH+GF+GH=EF′+EH+HG+GF″=HF′+HF″,
在Rt△HMF′中,HF′=$\sqrt{MF{′}^{2}+H{M}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
在Rt△HMF″中,HF″=$\sqrt{H{M}^{2}+F″{M}^{2}}$=$\sqrt{{8}^{2}+{5}^{2}}$=$\sqrt{89}$,
∴四边形EFGH的周长的最小值为10+$\sqrt{89}$;
探究2: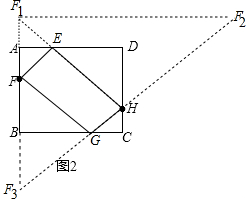
由题意可知四边形EFGH的周长的最小值=HF1+HF2,
易知HF1是Rt△F1F2F3的斜边的中线,
∴HF1=HF2=HF3,
在Rt△F1F2F3中,F1F2=16,F1F3=12,
∴F2F3=$\sqrt{1{2}^{2}+1{6}^{2}}$=20,
∴四边形EFGH的周长的最小值为20.
拓广探究:存在.理由如下:
如图2中,当四边形EFGH的周长最小时,四边形EFGH是平行四边形,易知:CH:CG:GH=3:4:5,设HC=3x,GC=4x,GH=5x,则DH=6-3x,BG=8-4x,
DE=$\frac{4}{3}$(6-3x),AE=8-$\frac{4}{3}$(6-3x),BF=$\frac{3}{4}$(8-4x),AF=6-$\frac{3}{4}$(8-4x),
∴S四边形EFGH=6×8-$\frac{1}{2}$•3x•4x-$\frac{1}{2}$•(6-3x)•$\frac{4}{3}$(6-3x)-$\frac{1}{2}$•[8-$\frac{4}{3}$(6-3x)]•[6-$\frac{3}{4}$(8-4x)]-$\frac{1}{2}$•(8-4x)•$\frac{3}{4}$(8-4x)
=-24x2+48x
=-24(x-1)2+24,
∵-24<0,
∴x=1时,四边形EFGH的面积最大,最大值为24.
点评 本题考查四边形综合题、轴对称的性质、勾股定理、二次函数等知识,解题的关键是灵活运用所学知识解决问题,学会构建二次函数解决最值问题,属于中考压轴题.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案 如图,将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,使点A,C,B′在同一条直线上,则旋转角的大小为( )
如图,将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,使点A,C,B′在同一条直线上,则旋转角的大小为( )| A. | 45° | B. | 90° | C. | 120° | D. | 135° |
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{7}{9}$ | D. | 1 |
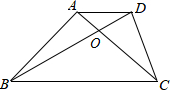 如图,梯形ABCD中,AD∥BC,∠BAC=90°,AB=AC,对角线AC与BD相交于点O,且BD=BC,那么∠BOC=105度.
如图,梯形ABCD中,AD∥BC,∠BAC=90°,AB=AC,对角线AC与BD相交于点O,且BD=BC,那么∠BOC=105度. 如图所示,点C是线段AB的黄金分割点,AC>BC,D、E分别是AC、BC的中点,仔细观察,试说明点DE黄金分割点.
如图所示,点C是线段AB的黄金分割点,AC>BC,D、E分别是AC、BC的中点,仔细观察,试说明点DE黄金分割点.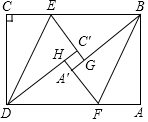 将一张矩形ABCD纸片,按如图进行折叠,分别在BC,AD两边上取两点E,F,使CE=AF,分别以DE,BF为对称轴将△CDE与△ABF翻折得到△C′DE′与△A′BF,且边EC′的延长线与A′B交于点G,边FA的延长线与C′D交于一点H,已知tan∠EBG=$\frac{3}{4}$,A′G=6,C′G=4,则线段BC=52.
将一张矩形ABCD纸片,按如图进行折叠,分别在BC,AD两边上取两点E,F,使CE=AF,分别以DE,BF为对称轴将△CDE与△ABF翻折得到△C′DE′与△A′BF,且边EC′的延长线与A′B交于点G,边FA的延长线与C′D交于一点H,已知tan∠EBG=$\frac{3}{4}$,A′G=6,C′G=4,则线段BC=52.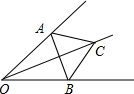 如图所示,OA=OB,AC=BC,求证:OC⊥AB.
如图所示,OA=OB,AC=BC,求证:OC⊥AB.