题目内容
9. 如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,连接AD.
如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,连接AD.(1)若∠BAD=45°,求证:△ACD为等腰三角形;
(2)若△ACD为直角三角形,求∠BAD的度数.
分析 (1)根据等腰三角形的性质求出∠B=∠C=30°,根据三角形内角和定理求出∠BAC=120°,求出∠CAD=∠ADC,根据等腰三角形的判定得出即可;
(2)有两种情况:①当∠ADC=90°时,当∠CAD=90°时,求出即可.
解答 (1)证明:∵AB=AC,∠B=30°,
∴∠B=∠C=30°,
∴∠BAC=180°-30°-30°=120°,
∵∠BAD=45°,
∴∠CAD=∠BAC-∠BAD=120°-45°=75°,∠ADC=∠B+∠BAD=75°,
∴∠ADC=∠CAD,
∴AC=CD,
即△ACD为等腰三角形;
(2)解:有两种情况:①当∠ADC=90°时,
∵∠B=30°,
∴∠BAD=∠ADC-∠B=90°-30°=60°;
②当∠CAD=90°时,∠BAD=∠BAC-∠CAD=120°-90°=30°;
即∠BAD的度数是60°或30°.
点评 本题考查了三角形内角和定理,等腰三角形的判定的应用,能根据定理求出各个角的度数是解此题的关键,用了分类讨论思想.

练习册系列答案
相关题目
19. 如图,△ABC中,AB=AC,∠BAC=120°,D是BC中点,DE⊥AB于点E,则BE是AE的( )
如图,△ABC中,AB=AC,∠BAC=120°,D是BC中点,DE⊥AB于点E,则BE是AE的( )
 如图,△ABC中,AB=AC,∠BAC=120°,D是BC中点,DE⊥AB于点E,则BE是AE的( )
如图,△ABC中,AB=AC,∠BAC=120°,D是BC中点,DE⊥AB于点E,则BE是AE的( )| A. | 1倍 | B. | 2倍 | C. | 3倍 | D. | 4倍 |
20. 在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证等式( )
在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证等式( )
 在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证等式( )
在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证等式( )| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | ||
| C. | a2-b2=(a+b)(a-b) | D. | (a+b)(a-2b)=a2-ab-2b2 |
17.若3x=15,3y=3,则3x-y=( )
| A. | 5 | B. | 3 | C. | 15 | D. | 10 |
 如图,A是线段MN的中点,B是线段MP的中点,且MN:NP=5:3,AB=3,求线段BN的长.
如图,A是线段MN的中点,B是线段MP的中点,且MN:NP=5:3,AB=3,求线段BN的长.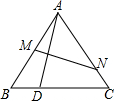 如图,点M、N分别是等边三角形ABC中AB,AC边上的点,点A关于MN的对称点落在BC边上的点D处.若$\frac{BD}{DC}$=$\frac{2}{3}$,则$\frac{AM}{AN}$的值$\frac{7}{8}$.
如图,点M、N分别是等边三角形ABC中AB,AC边上的点,点A关于MN的对称点落在BC边上的点D处.若$\frac{BD}{DC}$=$\frac{2}{3}$,则$\frac{AM}{AN}$的值$\frac{7}{8}$.
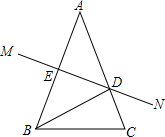 已知:如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
已知:如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.