题目内容

20．在边长为a的正方形中挖去一个边长为b的小正方形（a＞b）（如图甲），把余下的部分拼成一个矩形（如图乙），根据两个图形中阴影部分的面积相等，可以验证等式（　　）
A．（a+b）2=a2+2ab+b2B．（a-b）2=a2-2ab+b2
C．a2-b2=（a+b）（a-b）D．（a+b）（a-2b）=a2-ab-2b2

分析 第一个图形中阴影部分的面积计算方法是边长是a的正方形的面积减去边长是b的小正方形的面积，等于a2-b2；第二个图形阴影部分是一个长是（a+b），宽是（a-b）的长方形，面积是（a+b）（a-b）；这两个图形的阴影部分的面积相等．

解答 解：∵图甲中阴影部分的面积=a2-b2，图乙中阴影部分的面积=（a+b）（a-b），
而两个图形中阴影部分的面积相等，
∴阴影部分的面积=a2-b2=（a+b）（a-b）．
故选：C．

点评 此题主要考查了乘法的平方差公式．即两个数的和与这两个数的差的积等于这两个数的平方差，这个公式就叫做平方差公式．

练习册系列答案
相关题目
10．已知方程$\frac{1}{2}$x+b=0的解是x=-2，下列可能为直线y=$\frac{1}{2}$x+b的图象是（　　）
A．B．C．D．
11．如图，在△ABC中，∠ABC和∠ACB的平分线交于点F，过点F作EG∥BC分别交AB、AC于点E、G，若BE+CG=18，则线段EG的长为（　　）
A．16B．17C．18D．19
8．若方程（a+2b-5）xy+x-2y3a-b=8是关于x、y的二元一次方程，则a、b的值分别为（　　）
A．-1，2B．-1，-2C．1，-2D．1，2
15．乘法公式的探究及应用：
（1）如图1所示，阴影部分的面积是a2-b2（写成平方差的形式）

（2）若将图1中的阴影部分剪下来，拼成如图2所示的长方形，此长方形的面积是（a+b）（a-b）（写成多项式相乘的形式）．
（3）比较两图的阴影部分的面积，可以得到乘法公式：（a+b）（a-b）=a2-b2．
（4）应用所得的公式计算：2（1+$\frac{1}{2}$）（1+$\frac{1}{{2}^{2}}$）（1+$\frac{1}{{2}^{4}}$）（1+$\frac{1}{{2}^{8}}$）+$\frac{1}{{2}^{14}}$．
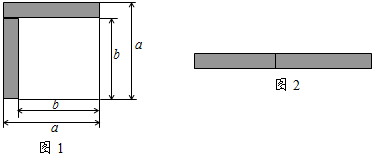
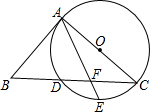5．如图，AC是⊙O的直径，BC交⊙O于点D，E是$\widehat{CD}$的中点，连接AE交BC于点F，∠ABC=2∠EAC．
（1）求证：AB是⊙O的切线；
（2）若tanB=$\frac{4}{3}$，BD=6，求CF的长．
12．据测定，海底扩张的速度是很缓慢的，在太平洋海底，某海沟的某处宽度为100米，某两侧的地壳向外扩张的速度是每年6厘米，假设海沟扩张速度恒定，扩张时间为x年，海沟的宽度为y米．
（1）写出海沟扩张时间x年与海沟的宽度y之间的表达式；
（2）你能计算以下当海沟宽度y扩张到400米时需要多少年吗？
9．如图，在△ABC中，AB=AC，D为BC上一点，∠B=30°，连接AD．
（1）若∠BAD=45°，求证：△ACD为等腰三角形；
（2）若△ACD为直角三角形，求∠BAD的度数．
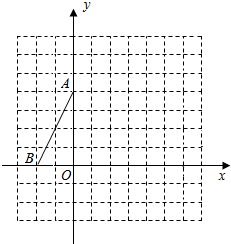6．如图，在平面直角坐标系中，O是坐标原点，点A、B的坐标分别为A（0，4）和B（-2，0），连结AB．
（1）现将△AOB绕点A按逆时针方向旋转90°得到△AO1B1，请画出△AO1B1，并直接写出点B1、O1的坐标（注：不要求证明）；
（2）求经过B、A、O1三点的抛物线对应的函数关系式，并画出抛物线的略图．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网