题目内容
19. 如图,△ABC中,AB=AC,∠BAC=120°,D是BC中点,DE⊥AB于点E,则BE是AE的( )
如图,△ABC中,AB=AC,∠BAC=120°,D是BC中点,DE⊥AB于点E,则BE是AE的( )| A. | 1倍 | B. | 2倍 | C. | 3倍 | D. | 4倍 |
分析 根据等腰三角形的性质可求得两底角的度数,再根据等腰三角形三线合一的性质可得到AD⊥BC,从而可利用直角三角形中30度的角所对的边是斜边的一半求得AE=$\frac{1}{2}$AD,AD=$\frac{1}{2}$AB,即可得出答案.
解答 解:∵AB=AC=8,∠BAC=120°,
∴∠B=∠C=30°,
∴∠BAD=60°,
∵AB=AC,D为BC中点,
∴AD⊥BC,
∴AD=$\frac{1}{2}$AB,
∵DE⊥AB,∠BAD=60°,
∴∠ADE=30°,
∴AE=$\frac{1}{2}$AD,
∴AE=$\frac{1}{4}$AB,
即BE=3AE.
故选C.
点评 此题主要考查等腰三角形的性质及含30度角的直角三角形的性质的综合运用,能求出AD=$\frac{1}{2}$AB和AE=$\frac{1}{2}$AD是解此题的关键.

练习册系列答案
相关题目
7.倒数是-3的数是( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
8.若方程(a+2b-5)xy+x-2y3a-b=8是关于x、y的二元一次方程,则a、b的值分别为( )
| A. | -1,2 | B. | -1,-2 | C. | 1,-2 | D. | 1,2 |
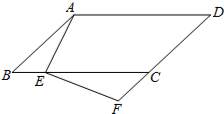 如图,在?ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.求证:BE•EC=FC•CD.
如图,在?ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.求证:BE•EC=FC•CD.



 如图所示,并按要求作图:
如图所示,并按要求作图: 如图,在△ABC中,∠ABC和∠ACB的平分线交于点F,过点F作EG∥BC分别交AB、AC于点E、G,若BE+CG=18,则线段EG的长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线交于点F,过点F作EG∥BC分别交AB、AC于点E、G,若BE+CG=18,则线段EG的长为( ) 如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,连接AD.
如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,连接AD.