题目内容
16．已知分式$\frac{6（m+3）}{{m}^{2}-9}$的值是正整数，则m的值为9或6或5或4．分析 根据平方差公式、分式的约分法则把原式化简，根据题意列式计算即可．
解答 解：$\frac{6（m+3）}{{m}^{2}-9}$=$\frac{6（m+3）}{（m+3）（m-3）}$=$\frac{6}{m-3}$，
当m-3=6或3或2或1时，分式$\frac{6（m+3）}{{m}^{2}-9}$的值是正整数，
解得，m=9或6或5或4，
故答案为：9或6或5或4．
点评 本题考查的是分式的化简求值，掌握分式的约分法则是解题的关键．
练习册系列答案
相关题目
11．下列计算正确的是（ ）
| A． | $\frac{1}{3a}$+$\frac{1}{3b}$=$\frac{1}{3（a+b）}$ | B． | $\frac{b}{a}$-$\frac{b+1}{a}$=$\frac{1}{a}$ | C． | $\frac{1}{a-b}$+$\frac{1}{b-a}$=0 | D． | $\frac{m}{a}$+$\frac{m}{b}$=$\frac{2m}{ab}$ |
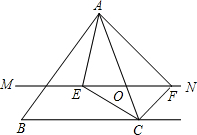△ABC中，点O是AC边上一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于E，交∠DCA的平分线于点F．
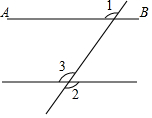已知，如图，∠1=120°，∠2=120°，求证：AB∥CD．