题目内容
1.已知函数y=kx+b的图象与y轴交点的纵坐标为-5,且当x=1,y=-2时,则此函数的解析式是y=3x-5.分析 根据函数y=kx+b的图象与y轴交点的纵坐标为-5,且当x=1时,y=-2可知此函数的图象过点(0,-5),(1,-2),再把两点代入函数解析式求出k、b的值即可.
解答 解:∵函数y=kx+b的图象与y轴交点的纵坐标为-5,且当x=1时,y=-2,
∴函数的图象过点(0,-5),(1,-2),
∴$\left\{\begin{array}{l}{b=-5}\\{k+b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=3}\\{b=-5}\end{array}\right.$,
故此函数的解析式为:y=3x-5.
故答案为:y=3x-5.
点评 本题考查的是一次函数图象上点的坐标特点,即一次函数图象上各点的坐标一定适合此函数的解析式.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目

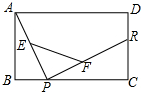 如图,矩形ABCD中,AD=13,DC=10,P是BC上的一点,R、E、F分别是DC、AP、RP的中点,当点P在BC上由B向C移动时,那么EF的长度$\frac{\sqrt{194}}{2}$.
如图,矩形ABCD中,AD=13,DC=10,P是BC上的一点,R、E、F分别是DC、AP、RP的中点,当点P在BC上由B向C移动时,那么EF的长度$\frac{\sqrt{194}}{2}$.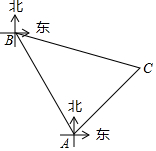 黄岩岛自古以来就是中国的领土,如图,为维护海洋利益,三沙市一艘海监船在黄岩岛附近海域巡航,某一时刻海监船在A处测得该岛上某一目标C在它的北偏东45°方向,海监船以30海里每小时的速度沿北偏西30°方向航行2小时后到达B处,此时测得该目标C在它的南偏东75°方向.求:
黄岩岛自古以来就是中国的领土,如图,为维护海洋利益,三沙市一艘海监船在黄岩岛附近海域巡航,某一时刻海监船在A处测得该岛上某一目标C在它的北偏东45°方向,海监船以30海里每小时的速度沿北偏西30°方向航行2小时后到达B处,此时测得该目标C在它的南偏东75°方向.求: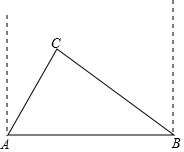 某县城在进行城市规划建设中,准备在相距1.6千米的两个超市A、B之间,扩建街道的宽度,但在A地的北偏东30°,B地的北偏西60°的C处有一半径为0.5千米的住宅小区,问在扩建公路时,这个小区是否有居民需要搬迁?($\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某县城在进行城市规划建设中,准备在相距1.6千米的两个超市A、B之间,扩建街道的宽度,但在A地的北偏东30°,B地的北偏西60°的C处有一半径为0.5千米的住宅小区,问在扩建公路时,这个小区是否有居民需要搬迁?($\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73) 如图,∠C=45°,D在CA的延长线上,∠DAB的平分线交CB的延长线于点E,若∠EAB=75°,则∠ABC的度数为105°.
如图,∠C=45°,D在CA的延长线上,∠DAB的平分线交CB的延长线于点E,若∠EAB=75°,则∠ABC的度数为105°.