题目内容
8.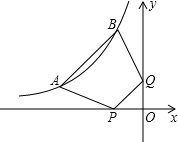 如图,点A(a,2)、B(-2,b)都在双曲线y=$\frac{k}{x}(x<0)$上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是y=x+$\frac{3}{2}$,则k=-7.
如图,点A(a,2)、B(-2,b)都在双曲线y=$\frac{k}{x}(x<0)$上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是y=x+$\frac{3}{2}$,则k=-7.
分析 作A点关于x轴的对称点C,B点关于y轴的对称点D,根据对称的性质得到C点、D点坐标.CD分别交x轴、y轴于P点、Q点,根据两点之间线段最短得此时四边形PABQ的周长最小,然后利用一次函数图象上点的坐标特征来求k的值.
解答  解:作A点关于x轴的对称点C,B点关于y轴的对称点D,所以C点坐标为(a,-2),D点坐标为(2,b),
解:作A点关于x轴的对称点C,B点关于y轴的对称点D,所以C点坐标为(a,-2),D点坐标为(2,b),
连结CD分别交x轴、y轴于P点、Q点,此时四边形PABQ的周长最小,
把C点的坐标代入y=x+$\frac{3}{2}$得到:-2=a+$\frac{3}{2}$,
解得a=-$\frac{7}{2}$,
则k=2a=-7.
故答案是:-7.
点评 本题考查了反比例函数图象上点的坐标特征、待定系数法求一次函数的解析式;熟练运用两点之间线段最短解决有关几何图形周长最短的问题.

练习册系列答案
相关题目
16.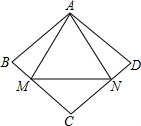 如图,已知四边形ABCD的四边相等,等边△AMN的顶点M、N分别在BC、CD上,且AM=AB,则∠C为( )
如图,已知四边形ABCD的四边相等,等边△AMN的顶点M、N分别在BC、CD上,且AM=AB,则∠C为( )
 如图,已知四边形ABCD的四边相等,等边△AMN的顶点M、N分别在BC、CD上,且AM=AB,则∠C为( )
如图,已知四边形ABCD的四边相等,等边△AMN的顶点M、N分别在BC、CD上,且AM=AB,则∠C为( )| A. | 100° | B. | 105° | C. | 110° | D. | 120° |
20.四边形ABCD中,AC⊥BD,AB、BC、CD、AD的中点分别是E、F、G、H,则四边形EFGH一定是( )
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 梯形 |
17.已知数据:6,6,x,4的众数与平均数相等,那么这组数据的极差是( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
 如图,在直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(2,0)
如图,在直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(2,0)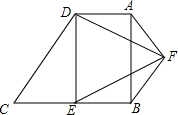 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,E是BC的中点,BC=2AD=$2\sqrt{3}$,△DEF是等边三角形,连结BF、AF.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,E是BC的中点,BC=2AD=$2\sqrt{3}$,△DEF是等边三角形,连结BF、AF.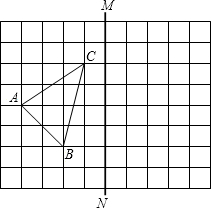 如图,在10×8的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
如图,在10×8的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).