题目内容
16.(1)已知m+n=8,mn=15,求m2-mn+n2的值.(2)已知a2+a-1=0,求a3+2a2+2016的值.
(3)已知a+$\frac{1}{a}$=$\sqrt{7}$,求a-$\frac{1}{a}$的值.
分析 (1)首先将m2-mn+n2配方,进而结合已知代入求出即可;
(2)由已知得到:a2=1-a,把a3变形为a•a2,把已知的式子表示出来,从而求代数式的值;
(3)把a+$\frac{1}{a}$=$\sqrt{7}$两边平方,求出a2+$\frac{1}{{a}^{2}}$的值,然后根据完全平方公式求出a2-2+$\frac{1}{{a}^{2}}$的值,再根据平方根的定义进行求解.
解答 解:(1)∵m+n=8,mn=15,
∴m2-mn+n2=(m+n)2-3mn=82-3×15=19.
即m2-mn+n2的值是19;
(2)∵a2+a-1=0,
∴a2=1-a,a2+a=1,
∴a3+2a2+2016
=a•a2+2a2+2016
=a(1-a)+2a2+2016
=a-a2+2a2+2016
=(a2+a)+2016
=1+2016
=2017;
(3)∵a+$\frac{1}{a}$=$\sqrt{7}$,
∴a2+$\frac{1}{{a}^{2}}$=7-2=5,
∴a2+$\frac{1}{{a}^{2}}$-2=3,
∴a-$\frac{1}{a}$=±$\sqrt{3}$.
点评 此题主要考查了配方法的应用,将原式正确配方得出是解题关键.(2)中把所求的式子用已知的式子表示出来.(3)考查了完全平方公式,利用好乘积二倍项不含字母是解题的关键.

练习册系列答案
相关题目

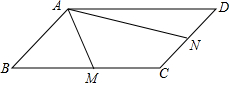 如图,在平行四边形ABCD中,M、N分别为BC、CD的中点,AM=1,AN=2,∠MAN=60°,则AB的长为$\frac{4}{3}$.
如图,在平行四边形ABCD中,M、N分别为BC、CD的中点,AM=1,AN=2,∠MAN=60°,则AB的长为$\frac{4}{3}$.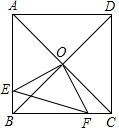 如图,已知正方形ABCD的对角线交于点O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF等于5.
如图,已知正方形ABCD的对角线交于点O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF等于5.