题目内容
5.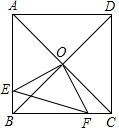 如图,已知正方形ABCD的对角线交于点O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF等于5.
如图,已知正方形ABCD的对角线交于点O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF等于5.
分析 由△BOF全等于△AOE,得到BF=AE=4,在直角△BEF中,从而求得EF的值.
解答 解:∵正方形ABCD中,OB=OC,∠BOC=∠EOF=90°,
∴∠EOB=∠FOC,
在△BOE和△COF中,
$\left\{\begin{array}{l}{∠OCB=∠OBE=45°}\\{OB=OC}\\{∠EOB=∠FOC}\end{array}\right.$,
∴△BOE和COF全等(ASA),
∴BF=AE=4,
∵AB=BC,
∴BE=CF=3,
在Rt△BEF中,BF=4,BE=3,
∴EF=5.
故答案为5;
点评 考查了正方形的性质,全等三角形的判定与性质和勾股定理,根据已知条件以及正方形的性质求证出两个全等三角形是解决本题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
20.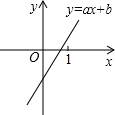 一次函数y=ax+b在直角坐标系中的图象如图所示,则化简$\sqrt{{{(a-b)}^2}}$-|a+b|的结果是( )
一次函数y=ax+b在直角坐标系中的图象如图所示,则化简$\sqrt{{{(a-b)}^2}}$-|a+b|的结果是( )
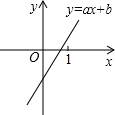 一次函数y=ax+b在直角坐标系中的图象如图所示,则化简$\sqrt{{{(a-b)}^2}}$-|a+b|的结果是( )
一次函数y=ax+b在直角坐标系中的图象如图所示,则化简$\sqrt{{{(a-b)}^2}}$-|a+b|的结果是( )| A. | 2a | B. | -2a | C. | 2b | D. | -2b |
10.在一年一度的国家学生体质测试中,金星中学对全校2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并绘制成统计表,绘制成频数直方图.
(1)在这个问题中,总体是什么?
(2)直接写出a,b,c,d的值.
(3)补全频数直方图.
(4)初中毕业生体能测试项目成绩评定标准是男生1000m不超过4′20″(即260秒)为合格,你能估计出该校初中男生的1000m的合格人数吗?如果能,请求出合格的人数;如果不能,请说明理由.

| 序号 | 范围(单位:秒) | 频数 | 频率 |
| 1 | 170<x≤200 | 5 | 0.1 |
| 2 | 200<x≤230 | 13 | a |
| 3 | 230<x≤260 | 15 | 0.3 |
| 4 | 260<x≤290 | c | d |
| 5 | 290<x≤320 | 5 | 0.1 |
| 6 | 320<x≤350 | 2 | 0.04 |
| 7 | 350<x≤380 | 2 | 0.04 |
| 合计 | b | 1.00 |
(2)直接写出a,b,c,d的值.
(3)补全频数直方图.
(4)初中毕业生体能测试项目成绩评定标准是男生1000m不超过4′20″(即260秒)为合格,你能估计出该校初中男生的1000m的合格人数吗?如果能,请求出合格的人数;如果不能,请说明理由.
17.-$\sqrt{17}$+1的小数部分是( )
| A. | -$\sqrt{17}$+5 | B. | -$\sqrt{17}$+4 | C. | -$\sqrt{17}$-3 | D. | $\sqrt{17}$-4 |
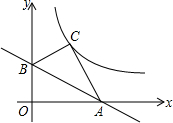 如图,已知点A(6,0),B(0,2$\sqrt{3}$),O为坐标原点,点O关于直线AB的对称点C恰好落在反比例函数y=$\frac{k}{x}$(k>0)的图象上,求k的值.
如图,已知点A(6,0),B(0,2$\sqrt{3}$),O为坐标原点,点O关于直线AB的对称点C恰好落在反比例函数y=$\frac{k}{x}$(k>0)的图象上,求k的值.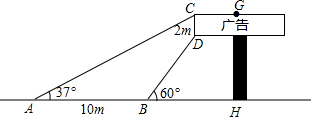 如图,长方形广告牌架在楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75,$\sqrt{3}$≈1.732,结果精确到0.1m)
如图,长方形广告牌架在楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75,$\sqrt{3}$≈1.732,结果精确到0.1m)