题目内容
11.操作与探究综合实践课,老师把一个足够大的等腰直角三角尺AMN靠在一个正方形纸片ABCD的一侧,使边AM与AD在同
一直线上(如图1),其中∠AMN=90°,AM=MN.
(1)猜想发现
老师将三角尺AMN绕点A逆时针旋转α.如图2,当0<α<45°时,边AM,AN分别与直线BC,CD交于点E,F,连结EF.小明同学探究发现,线段EF,BE,DF满足EF=BE-DF;如图3,当45°<α<90°时,其它条件不变.
①填空:∠DAF+∠BAE=45度;
②猜想:线段EF,BE,DF三者之间的数量关系是:EF=BE+DF.
(2)证明你的猜想;
(3)拓展探究
在45°<α<90°的情形下,连结BD,分别交AM,AN于点G,H,如图4连结EH,试证明:EH⊥AN.

分析 (1)①由全等三角形的性质即可得出结论;
②由全等三角形的性质即可得出答案;
(2)延长CB至点K,使BK=DF,连结AK,由SAS证明△ABK≌△ADF,得出AK=AF,∠BAK=∠DAF.由等腰直角三角形的性质得出∠MAN=∠N=45°,即可证出∠DAF+∠BAE=45°.证出∠EAF=∠EAK.由SAS证明△AEF≌△AEK,得出EF=EK.即可得出EF=BE+DF.
(3)连结AC.证明△ADH∽△ACE.得出$\frac{AD}{AH}=\frac{AC}{AE}$,再证明△ADC∽△AHE.得出∠ADC=∠AHE=90°.即可得出结论.
解答 (1)解:①∠DAF+∠BAE=45°;
故答案为:45;
②线段EF,BE,DF三者之间的数量关系是EF=BE+DF;
故答案为:EF=BE+DF;
(2)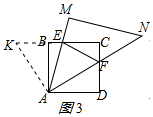 证明:如图3,延长CB至点K,使BK=DF,连结AK.
证明:如图3,延长CB至点K,使BK=DF,连结AK.
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ABK=∠D=90°.
在△ABK和△ADF中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠ABK=∠D}&{\;}\\{BK=DF}&{\;}\end{array}\right.$,
∴△ABK≌△ADF(SAS),
∴AK=AF,∠BAK=∠DAF.
∵∠AMN=90°,AM=MN,
∴∠MAN=∠N=45°,
∴∠DAF+∠BAE=45°.
∴∠EAK=∠BAK+∠BAE=45°,
∴∠EAF=∠EAK.
在△AEF和△AEK中,$\left\{\begin{array}{l}{AF=AK}&{\;}\\{∠EAF=∠EAK}&{\;}\\{AE=AE}&{\;}\end{array}\right.$,
∴△AEF≌△AEK(SAS).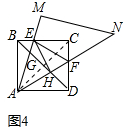
∴EF=EK.
∴EF=BE+DF.
(3)证明:如图4,连结AC.
∵四边形ABCD是正方形,
∴∠ACE=∠ADH=∠CAD=45°.
∵∠EAF=45°,
∴∠EAF=∠CAD=45°.
∴∠CAE=∠DAH,
∴△ADH∽△ACE.
∴$\frac{AD}{AC}=\frac{AH}{AE}$.
∴$\frac{AD}{AH}=\frac{AC}{AE}$,
又∵∠CAD=∠EAF=45°,
∴△ADC∽△AHE.
∴∠ADC=∠AHE=90°.
∴EH⊥AN.
点评 本题是四边形综合题目,考查了正方形的性质,全等三角形的性质和判定,相似三角形的判定与性质等知识;本题综合性强,有一定难度,证明三角形全等和三角形相似是解决问题的关键.

| 一周内累计的读书时间(小时) | 5 | 8 | 10 | 14 |
| 人数(个) | 1 | 7 | 5 | 3 |
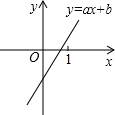 一次函数y=ax+b在直角坐标系中的图象如图所示,则化简$\sqrt{{{(a-b)}^2}}$-|a+b|的结果是( )
一次函数y=ax+b在直角坐标系中的图象如图所示,则化简$\sqrt{{{(a-b)}^2}}$-|a+b|的结果是( )| A. | 2a | B. | -2a | C. | 2b | D. | -2b |
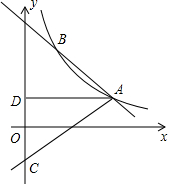 如图,反比例函数y=$\frac{k}{x}$(x>0)图象经过点A(2$\sqrt{3}$,1),直线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
如图,反比例函数y=$\frac{k}{x}$(x>0)图象经过点A(2$\sqrt{3}$,1),直线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.