题目内容
5.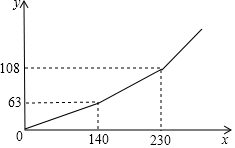 为促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中的折线反映了每户居民每月用电电费y(单位:元)与用电量x(单位:度)间的函数关系.
为促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中的折线反映了每户居民每月用电电费y(单位:元)与用电量x(单位:度)间的函数关系.(1)根据图象,阶梯电价方案分为三个档次,请填写下表:
| 档次 | 第一档 | 第二档 | 第三档 |
| 每月用电量x(度) | 0<x≤140 | 140<x≤230 | x>230 |
(3)求第二档每月电费y(元)与用电量x(单位:度)之间的函数表达式;
(4)在每月用电量超过230度时,每度电比第二档多m元,小刚家某月用电290度,缴纳电费153元,求m的值.
分析 (1)利用函数图象可以得出,阶梯电价方案分为三个档次,利用横坐标可得出:第二档,第三档中x的取值范围;
(2)根据第一档范围是:0<x≤140,利用图象上点的坐标得出解析式,进而得出x=70时,求出y的值;
(3)设第二档每月电费y(元)与用电量x(度)之间的函数关系式为:y=ax+c,将(140,63),(230,108)代入得出即可;
(4)分别求出第二、三档每度电的费用,进而得出m的值即可.
解答 解:(1)利用函数图象可以得出,阶梯电价方案分为三个档次,利用横坐标可得出:
第二档:140<x≤230,第三档x>230;
(2)根据第一档范围是:0<x≤140,
根据图象上点的坐标得出:设解析式为:y=kx,将(140,63)代入得出:k=$\frac{63}{140}$=0.45,
故y=0.45x,
当x=70,y=0.45×70=31.5(元),
故答案为:31.5;
(3)设第二档每月电费y(元)与用电量x(度)之间的函数关系式为:y=ax+c,
将(140,63),(230,108)代入得出:$\left\{\begin{array}{l}{140a+c=63}\\{230a+c=108}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{c=-7}\end{array}\right.$,
则第二档每月电费y(元)与用电量x(度)之间的函数关系式为:y=$\frac{1}{2}$x-7(140<x≤230);
(4)根据图象可得出:用电230度,需要付费108元,用电140度,需要付费63元,
故,108-63=45(元),230-140=90(度),
45÷90=0.5(元/度),
则第二档电费为0.5元/度;
∵小刚家某月用电290度,交电费153元,
290-230=60(度),153-108=45(元),
45÷60=0.75(元/度),
m=0.75-0.5=0.25,
答:m的值为0.25.
点评 此题主要考查了一次函数的应用以及待定系数法求一次函数解析式,利用图象获取正确信息是解题关键.

 名校课堂系列答案
名校课堂系列答案| A. | 由3+x=5,得x=5+3 | B. | 由7x=$\frac{1}{7}$,得x=49 | C. | 由$\frac{1}{2}$y=0,得y=2 | D. | 由3=x-2,得x=2+3 |
| A. | x>-2 | B. | x≤-2 | C. | x<-2 | D. | x≥-2 |
| A. | 1.56×104m | B. | 15.6×103m | C. | 0.156×104m | D. | 1.56×102m |
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{9}+\sqrt{4}=\sqrt{5}$ | C. | $\sqrt{8}+\sqrt{2}=3\sqrt{2}$ | D. | $\sqrt{{{({-5})}^2}}=-5$ |