题目内容
如图，四边形ABCD中，AB∥CD，∠ABC=∠CDA，求证：四边形ABCD为平行四边形．考点：平行四边形的判定,全等三角形的判定与性质
专题：证明题
分析：首先证得△ABC≌△ACD，利用全等三角形的性质得到AB=CD，AB∥CD，从而判定四边形ABCD为平行四边形．
解答：证明：∵AB∥CD，
∴∠BAC=∠ACD，
在△ABC和△ACD中
∴△ABC≌△ACD，
∴AB=CD，
∴AB=CD，AB∥CD，
∴四边形ABCD为平行四边形．
∴∠BAC=∠ACD，
在△ABC和△ACD中
|
∴△ABC≌△ACD，
∴AB=CD，
∴AB=CD，AB∥CD，
∴四边形ABCD为平行四边形．
点评：本题主要考查全等三角形的判定定理，关键在于熟练掌握判定定理AAS．
练习册系列答案
相关题目
如图，若a∥b，∠1=50°，则∠2=（ ）| A、50° | B、130° |
| C、60° | D、120° |
实数a，b，c是数轴上三点A，B，C所对应的数，如图，化简：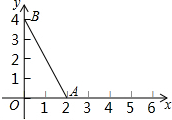
△OAB的三个顶点坐标分别是O（0，0），A（2，0），B（0，4）．
在直角坐标系中，△ABC的三个顶点的位置如图所示，现将△ABC沿AA′的方向平移，使得点A移至图中的点A′的位置．