题目内容
18.解方程:(1)(2x+3)2-16=0;
(2)x2+4x-4=0(用配方法)
(3)(x-3)2-2x(x-3)=0;
(4)3y2+4y-4=0.
分析 (1)直接开平方法求解可得;
(2)配方法求解可得;
(3)因式分解法求解可得;
(4)因式分解法求解可得.
解答 解:(1)(2x+3)2=16,
2x+3=±4,
即2x+3=4或2x+3=-4,
解得:x=$\frac{1}{2}$或x=-$\frac{7}{2}$;
(2)x2+4x=4,
x2+4x+4=4+4,即(x+2)2=8,
∴x+2=$±2\sqrt{2}$,
∴x=-2$±2\sqrt{2}$;
(3)(x-3)(x-3-2x)=0,
即(x-3)(-x-3)=0,
∴x-3=0或-x-3=0,
解得:x=3或x=-3;
(4)(y+2)(3y-2)=0,
∴y+2=0或3y-2=0,
解得:y=-2或y=$\frac{2}{3}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
9.已知点(-2,y1),(-1,y2),(3,y3)在函数y=(x+1)2+a的图象上,则y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y3>y1>y2 | C. | y3>y2>y1 | D. | y2>y1>y3 |
10.与-3x2y是同类项的是( )
| A. | -2x2y | B. | -3xy2 | C. | 2x3y | D. | 5xy |
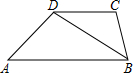 如图所示,在梯形ABCD中,AB∥CD,BD2=AB•DC,求证:∠A=∠CBD.
如图所示,在梯形ABCD中,AB∥CD,BD2=AB•DC,求证:∠A=∠CBD.