题目内容
4. 证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
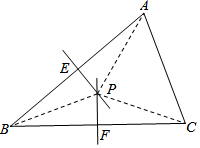
证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.已知:如图,在△ABC中,分别作AB边、BC边的垂直平分线,两线相交于点P,分别交AB边、BC边于点E、F.
求证:AB、BC、AC的垂直平分线相交于点P
证明:∵点P是AB边垂直平线上的一点,
∴PB=PA(垂直平分线上任意一点,到线段两端点的距离相等).
同理可得,PB=PC.
∴PA=PC(等量代换).
∴点P在AC的垂直平分线上,(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
∴AB、BC、AC的垂直平分线相交于点P,且PA=PB=PC.
分析 根据线段垂直平分线的性质可得出PB=PA,同理可得出PA=PC,由此即可得出PA=PC,再根据线段垂直平分线的性质可得出点P是AC边垂直平线上的一点,从而证出结论.
解答  证明:∵点P是AB边垂直平线上的一点,
证明:∵点P是AB边垂直平线上的一点,
∴PB=PA (垂直平分线上任意一点,到线段两端点的距离相等).
同理可得,PB=PC.
∴PA=PC(等量代换).
∴点P是AC边垂直平线上的一点(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上),
∴AB、BC、AC的垂直平分线相交于点P,且PA=PB=PC.
故答案为:PB;PA;垂直平分线上任意一点,到线段两端点的距离相等;PC;PA;PC;点P在AC的垂直平分线上,垂直平分线上;PA=PB=PC.
点评 本题考查了线段垂直平分线的性质,解题的关键是找出点P是AC边垂直平线上的一点.解决该题型题目时,根据线段垂直平分线的性质找出相等的线段是关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 中,当
中,当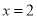 时,
时, 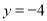 ;当
;当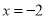 时,
时,  ,则这个等式中
,则这个等式中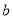 与
与 的值分别是( )
的值分别是( ) =3,
=3, 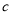 =2 B.
=2 B.  =-3,
=-3, 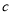 =-2 C.
=-2 C. 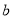 =-3,
=-3,  =2 D.
=2 D.  =3,
=3, 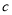 =-2
=-2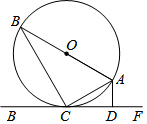 如图,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D.
如图,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D.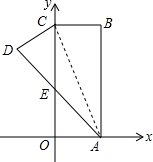 如图,在平面直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,点B落在点D的位置,且AD交y轴于点E,那么点D的坐标为(-$\frac{4}{5}$,$\frac{12}{5}$).
如图,在平面直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,点B落在点D的位置,且AD交y轴于点E,那么点D的坐标为(-$\frac{4}{5}$,$\frac{12}{5}$).