题目内容
12.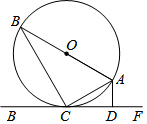 如图,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D.
如图,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D.(1)求证:∠CAD=∠BAC.
(2)若∠CAD=30°,AD=2,求BC的长.
分析 (1)连接OC,可证明AD∥OC,可求得∠OCA=∠CAD,再由OC=OA可得∠OCA=∠BAC,可证得结论;
(2)由(1)可求得∠BAC=30°,在Rt△ACD中可求得AC,在Rt△ACB中可求得BC.
解答 (1)证明:
连接OC,如图,
∵EF是⊙O的切线,
∴OC⊥EF,
∵AD⊥EF,
∴OC∥AD,
∴∠OCA=∠CAD,
∵OC=OA,
∴∠OCA=∠BAC,
∴∠CAD=∠BAC;
(2)解:
∵AD⊥EF,∠CAD=30°,AD=2,
∴AC=2AD=4,
∵AB是⊙O的直径,
∴∠ACB=90°,
由(1)可知∠BAC=∠CAD=30°,
∴AB=2AC=8,
在Rt△ABC中,由勾股定理可得BC=4$\sqrt{3}$.
点评 本题主要考查切线的性质,掌握过切点的半径垂直切线是解题的关键.

练习册系列答案
相关题目
3.已知$\frac{xyz}{{|{xyz}|}}$=1,则$\frac{|x|}{x}$+$\frac{y}{|y|}$+$\frac{|z|}{z}$值为多少( )
| A. | 1或-3 | B. | 1或-1 | C. | -1或3 | D. | 3或-3 |
7.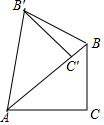 如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠C′B′B的度数为( )
如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠C′B′B的度数为( )
 如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠C′B′B的度数为( )
如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠C′B′B的度数为( )| A. | 40° | B. | 20° | C. | 70° | D. | 50° |

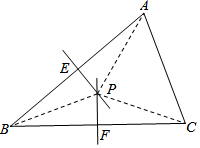 证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.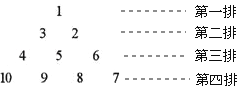 将正整数按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示9,则表示58的有序数对是(11,9 )
将正整数按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示9,则表示58的有序数对是(11,9 )