题目内容
19.阅读材料,大数学家高斯在上学读书时曾经研究过这样一个问题,1+2+3+…10=?经过研究,这个问题的一般结论是1+2+3+…+n=$\frac{1}{2}$n(n+1),其中n是正整数,现在我们来研究一个类似的问题:1×2+2×3+…+n(n+1)=?
观察下面三个特殊的等式:
1×2=$\frac{1}{3}$(1×2×3-0×1×2)
2×3=$\frac{1}{3}$(2×3×4-1×2×3)
3×4=$\frac{1}{3}$(3×4×5-2×3×4)
将这三个等式的两边相加,可以得到1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=20
读完这段材料,请你计算:
(1)1×2+2×3+…+100×101
(2)1×2+2×3+…+n(n+1)
(3)1×2×3+2×3×4+…+n(n+1)(n+2)
分析 (1)根据题目中的信息可以解答本题;
(2)根据题目中的信息可以解答本题;
(3)根据题目中的信息,运用类比的数学思想可以解答本题.
解答 解:(1)1×2+2×3+…+100×101
=$\frac{1}{3}×100×101×102$
=343400;
(2)1×2+2×3+…+n(n+1)=$\frac{1}{3}n(n+1)(n+2)$;
(3)1×2×3+2×3×4+…+n(n+1)(n+2)
=$\frac{1}{4}(1×2×3×4-0×1×2×3)$+$\frac{1}{4}(2×3×4×5-1×2×3×4)$+…+$\frac{1}{4}$[n(n+1)(n+2)(n+3)-(n-1)n(n+1)(n+2)]
=$\frac{1}{4}$n(n+1)(n+2)(n+3).
点评 本题考查数字的变化类,解题的关键是明确题意,发现数字的变化规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.抛物线y=-2(x-1)2-3的最大值为( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
7.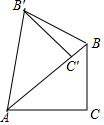 如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠C′B′B的度数为( )
如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠C′B′B的度数为( )
 如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠C′B′B的度数为( )
如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠C′B′B的度数为( )| A. | 40° | B. | 20° | C. | 70° | D. | 50° |
9. 一个正方体的表面展开图如图所示,每个面上都写有文字,则“爱”字的对面上的文字是( )
一个正方体的表面展开图如图所示,每个面上都写有文字,则“爱”字的对面上的文字是( )
 一个正方体的表面展开图如图所示,每个面上都写有文字,则“爱”字的对面上的文字是( )
一个正方体的表面展开图如图所示,每个面上都写有文字,则“爱”字的对面上的文字是( )| A. | 我 | B. | 校 | C. | 蜀 | D. | 学 |
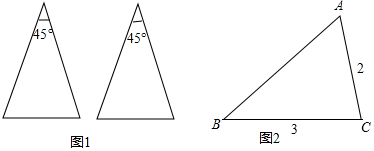
 是关于
是关于 的方程
的方程 的一个解,则
的一个解,则 =_________
=_________
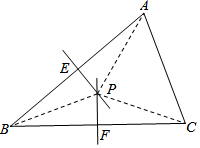 证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.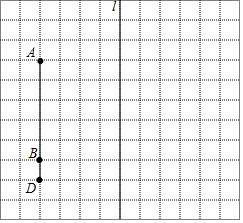 如图,在正方形网格中,每个小正方形的边长为1个单位长度.线段AD的两个端点都在格点上,点B是线段AD上的格点,且BD=1,直线l在格线上.
如图,在正方形网格中,每个小正方形的边长为1个单位长度.线段AD的两个端点都在格点上,点B是线段AD上的格点,且BD=1,直线l在格线上.