题目内容
20.学习圆锥有关知识的时候,王老师要求每个同学都做一个圆锥模型,小华用家里的就纸板做了一个底面半径为3cm,母线长为5cm的圆锥模型,则此圆锥的侧面积是15πcm2.分析 圆锥的侧面积=底面周长×母线长÷2,依此列式计算即可求解.
解答 解:底面圆的半径为3cm,则底面周长=6πcm,侧面面积=$\frac{1}{2}$×6π×5=15πcm2.
故此圆锥的侧面积是15πcm2.
故答案为:15π.
点评 考查了圆锥的计算,本题利用了圆的周长公式和扇形面积公式求解.

练习册系列答案
相关题目
11.已知2<x<3,化简:$\sqrt{({x-1)}^{2}}$+|x-3|的结果是( )
| A. | 2x-5 | B. | 5-2x | C. | -1 | D. | 2 |
8.已知⊙O的半径为r,其内接正六边形,正四边形,正三角形的边长分别为a,b,c,则a:b:c的值为( )
| A. | 1:2:3 | B. | 3:2:1 | C. | 1:$\sqrt{2}$:$\sqrt{3}$ | D. | $\sqrt{3}$:$\sqrt{2}$:1 |
12.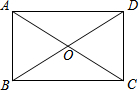 如图,四边形ABCD的对角线AC,BD相交于点O,且AC=BD,则下列条件能判定四边形ABCD为矩形的是( )
如图,四边形ABCD的对角线AC,BD相交于点O,且AC=BD,则下列条件能判定四边形ABCD为矩形的是( )
 如图,四边形ABCD的对角线AC,BD相交于点O,且AC=BD,则下列条件能判定四边形ABCD为矩形的是( )
如图,四边形ABCD的对角线AC,BD相交于点O,且AC=BD,则下列条件能判定四边形ABCD为矩形的是( )| A. | AB=CD | B. | OA=OC,OB=OD | C. | AC⊥BD | D. | AB∥CD,AD=BC |
7.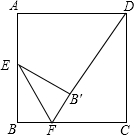 如图,正方形ABCD边长为2,E为AB边的中点,点F是BC边上一个动点,把△BEF沿EF向形内部折叠,点B的对应点为B′,当B′D的长最小时,BF长为( )
如图,正方形ABCD边长为2,E为AB边的中点,点F是BC边上一个动点,把△BEF沿EF向形内部折叠,点B的对应点为B′,当B′D的长最小时,BF长为( )
 如图,正方形ABCD边长为2,E为AB边的中点,点F是BC边上一个动点,把△BEF沿EF向形内部折叠,点B的对应点为B′,当B′D的长最小时,BF长为( )
如图,正方形ABCD边长为2,E为AB边的中点,点F是BC边上一个动点,把△BEF沿EF向形内部折叠,点B的对应点为B′,当B′D的长最小时,BF长为( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$-1 | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{5}+1}{2}$ |
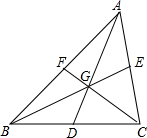 如图,△ABC的三条中线相交于点G.
如图,△ABC的三条中线相交于点G.