如图.矩形OABC的顶点A.C分别在x轴和y轴上.点B的坐标为(2.3).反比例函数y=$\frac{k}{x}$的图象经过BC的中点D.且与AB交于点E.连接DE．(1)求反比例函数的表达式及点E的坐标,(2)点F是OC边上一点.若△FBC∽△DEB.求直线FB的解析式,的条件下.若点P是反比例函数y=$\frac{k}{x}$的图象上的一点.若△PCF的面积恰好等于矩� 题目和参考答案——青夏教育精英家教网—

题目内容

16．

如图，矩形OABC的顶点A，C分别在x轴和y轴上，点B的坐标为（2，3），反比例函数y=$\frac{k}{x}$（k＞0）的图象经过BC的中点D，且与AB交于点E，连接DE．
（1）求反比例函数的表达式及点E的坐标；
（2）点F是OC边上一点，若△FBC∽△DEB，求直线FB的解析式；
（3）在（2）的条件下，若点P是反比例函数y=$\frac{k}{x}$（x＞0）的图象上的一点，若△PCF的面积恰好等于矩形OABC的面积，求P点的坐标．

分析（1）首先根据点B的坐标和点D为BC的中点表示出点D的坐标，代入反比例函数的解析式求得k值，然后将点E的横坐标代入求得E点的纵坐标即可；
（2）根据△FBC∽△DEB，利用相似三角形对应边的比相等确定点F的坐标后即可求得直线FB的解析式．
（3）先求出CF，再用△PCF的面积恰好等于矩形OABC的面积，求出PG（点P横坐标）即可．

解答解：（1）∵BC∥x轴，点B的坐标为（2，3），
∴BC=2，
∵点D为BC的中点，
∴CD=1，
∴点D的坐标为（1，3），
代入双曲线y=$\frac{k}{x}$（x＞0）得k=1×3=3；
∴反比例函数的表达式y=$\frac{3}{x}$，
∵BA∥y轴，
∴点E的横坐标与点B的横坐标相等为2，
∵点E在双曲线上，
∴y=$\frac{3}{2}$，
∴点E的坐标为（2，$\frac{3}{2}$）；
（2）∵点E的坐标为（2，$\frac{3}{2}$），B的坐标为（2，3），点D的坐标为（1，3），
∴BD=1，BE=$\frac{3}{2}$，BC=2
∵△FBC∽△DEB，
∴$\frac{CF}{DB}=\frac{BC}{EB}$．
即：$\frac{CF}{1}=\frac{2}{\frac{3}{2}}$，
∴FC=$\frac{4}{3}$，
∴点F的坐标为（0，$\frac{5}{3}$），
设直线FB的解析式y=kx+b（k≠0）
则$\left\{\begin{array}{l}{2k+b=3}\\{b=\frac{5}{3}}\end{array}\right.$，
解得：k=$\frac{2}{3}$，b=$\frac{5}{3}$，
∴直线FB的解析式y=$\frac{2}{3}$x+$\frac{5}{3}$，
（3）如图，过点P作PG⊥y轴，

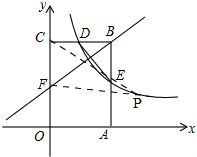
由（2）有，直线FB的解析式y=$\frac{2}{3}$x+$\frac{5}{3}$，
∴F（0，$\frac{5}{3}$），
∵C（0，3），
∴CF=3-$\frac{5}{3}$=$\frac{4}{3}$，
∵矩形OABC的顶点A，C分别在x轴和y轴上，点B的坐标为（2，3），
∴OA=2，OC=3，
∴S_矩形OABC=2×3=6，
∵若△PCF的面积恰好等于矩形OABC的面积，
∴S_△PCF=6，
∴S_△PCF=$\frac{1}{2}$×CF×PG=$\frac{1}{2}$×$\frac{4}{3}$×PG=6，
∴PG=9，
∵点P是反比例函数y=$\frac{3}{x}$（x＞0）的图象上的一点，
∴P（9，$\frac{1}{3}$）．