题目内容
19.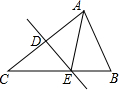 如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )
如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )| A. | 10 | B. | 13 | C. | 16 | D. | 19 |
分析 根据线段的垂直平分线的概念和性质得到EA=EC,AC=2AD=6,根据三角形的周长公式计算即可.
解答 解:∵DE垂直平分AC,
∴EA=EC,AC=2AD=6,
△ABE的周长=AE+BE+AB=CE+BE+AB=BC+AB=13,
∴△ABC的周长=AC+BC+AB=19,
故选:D.
点评 本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
9.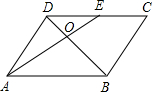 如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )
如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )
 如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )
如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )| A. | 24cm2 | B. | 36cm2 | C. | 48cm2 | D. | 60cm2 |
7.下列条件能判断点M是线段AB中点的是( )
| A. | AM=BM | B. | AM=BM=$\frac{1}{2}$AB | C. | AM=$\frac{1}{2}$AB | D. | AM+BM=AB |
11. 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=3,则PQ的最小值为( )
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=3,则PQ的最小值为( )
 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=3,则PQ的最小值为( )
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=3,则PQ的最小值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 无法确定 |
9.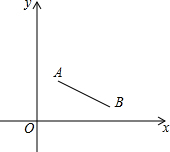 如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
 如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )| A. | (1,-5) | B. | (5,-2) | C. | (5,-1) | D. | (-1,5) |
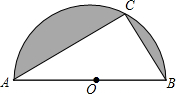 如图,半圆的直径AB,点C在半圆上,已知半径为1,△ABC的周长为$\sqrt{5}$+2,则阴影部分的面积为$\frac{1}{2}π-\frac{1}{4}$.
如图,半圆的直径AB,点C在半圆上,已知半径为1,△ABC的周长为$\sqrt{5}$+2,则阴影部分的面积为$\frac{1}{2}π-\frac{1}{4}$.