题目内容
3.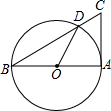 如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )
如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )| A. | 70° | B. | 35° | C. | 20° | D. | 40° |
分析 先依据切线的性质求得∠CAB的度数,然后依据直角三角形两锐角互余的性质得到∠CBA的度数,然后由圆周角定理可求得∠AOD的度数.
解答 解:∵AC是圆O的切线,AB是圆O的直径,
∴AB⊥AC.
∴∠CAB=90°.
又∵∠C=70°,
∴∠CBA=20°.
∴∠DOA=40°.
故选:D.
点评 本题主要考查的是切线的性质、圆周角定理、直角三角形的性质,求得∠CBA=20°是解题的关键.

练习册系列答案
相关题目
8.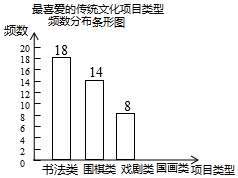 某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
最喜爱的传统文化项目类型频数分布表
根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布条形图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
 某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.最喜爱的传统文化项目类型频数分布表
| 项目类型 | 频数 | 频率 |
| 书法类 | 18 | a |
| 围棋类 | 14 | 0.28 |
| 喜剧类 | 8 | 0.16 |
| 国画类 | b | 0.20 |
(1)直接写出频数分布表中a的值;
(2)补全频数分布条形图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
15.若一个三角形的两边长分别为3和7,则第三边长可能是( )
| A. | 6 | B. | 3 | C. | 2 | D. | 11 |
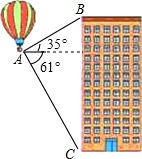 热气球的探测器显示,从热气球所在位置A处看一栋楼顶部B处的仰角为35°,看这栋楼底部C处的俯角为61°,已知这栋楼BC的高度为300m,求热气球所在位置距地面的距离(结果保留整数).(参考数据:tan35°≈0.70,tan61°≈1.80)
热气球的探测器显示,从热气球所在位置A处看一栋楼顶部B处的仰角为35°,看这栋楼底部C处的俯角为61°,已知这栋楼BC的高度为300m,求热气球所在位置距地面的距离(结果保留整数).(参考数据:tan35°≈0.70,tan61°≈1.80)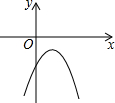 已知二次函数y=-(x-a)2-b的图象如图所示,则反比例函数y=$\frac{ab}{x}$与一次函数y=ax+b的图象可能是( )
已知二次函数y=-(x-a)2-b的图象如图所示,则反比例函数y=$\frac{ab}{x}$与一次函数y=ax+b的图象可能是( )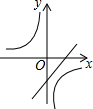
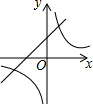
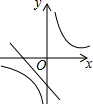
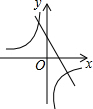
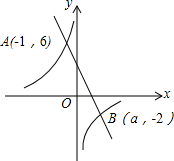 如图,一次函数y1=kx+b(k≠0)和反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于点A(-1,6),B(a,-2).
如图,一次函数y1=kx+b(k≠0)和反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于点A(-1,6),B(a,-2).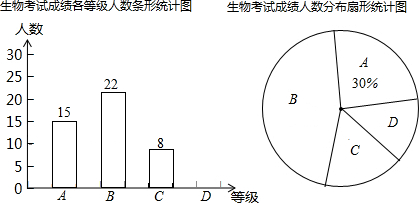
 在⊙O中,弦AB=3,将AB绕点O逆时针旋转60°得弦A′B′,连接OA′,已知OA′⊥AB于C,求⊙O的半径.
在⊙O中,弦AB=3,将AB绕点O逆时针旋转60°得弦A′B′,连接OA′,已知OA′⊥AB于C,求⊙O的半径.