题目内容
18.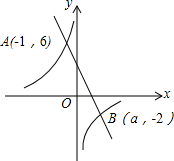 如图,一次函数y1=kx+b(k≠0)和反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于点A(-1,6),B(a,-2).
如图,一次函数y1=kx+b(k≠0)和反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于点A(-1,6),B(a,-2).(1)求一次函数与反比例函数的解析式;
(2)根据图象直接写出y1>y2时,x的取值范围.
分析 (1)把点A坐标代入反比例函数求出k的值,也就求出了反比例函数解析式,再把点B的坐标代入反比例函数解析式求出a的值,得到点B的坐标,然后利用待定系数法即可求出一次函数解析式;
(2)找出直线在一次函数图形的上方的自变量x的取值即可.
解答 解:(1)把点A(-1,6)代入反比例函数y2=$\frac{m}{x}$(m≠0)得:
m=-1×6=-6,
∴${y}_{2}=-\frac{6}{x}$.
将B(a,-2)代入${y}_{2}=-\frac{6}{x}$得:
-2=$\frac{-6}{a}$,
a=3,
∴B(3,-2),
将A(-1,6),B(3,-2)代入一次函数y1=kx+b得:
$\left\{\begin{array}{l}{-k+b=6}\\{3k+b=-2}\end{array}\right.$
∴$\left\{\begin{array}{l}{k=-2}\\{b=4}\end{array}\right.$
∴y1=-2x+4.
(2)由函数图象可得:x<-1或0<x<3.
点评 本题考查了反比例函数与一次函数的交点问题,待定系数法求函数解析式,此类题目的求解一般都是先把已知点的坐标代入反比例函数表达式求出反比例函数解析式,然后再求一次函数解析式,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.青少年“心理健康”问题越来越引起社会的广泛关注,某区为了解学生的心理健康状况,对中学初二学生进行了一次“心理健康”知识测试,随机抽取了部分学生的成绩作为样本,绘制了频率分布表和频率分布直方图的一部分.
学生心理健康测试成绩频率统计表
请解答下列问题:
(1)学生心理健康测试成绩频率统计表中的m=16;
(2)请补全学生心理健康测试成绩频数统计图;
(3)若成绩在60分以下(不含60分)心理健康状况为不良,60分-70分(含60分)为一般,70分-90分(含70分)为良好,90分(含90分)以上为优秀,请补全学生心理健康状况扇形统计图.

学生心理健康测试成绩频率统计表
| 分 组 | 频数 | 频率 |
| 50~60 | 4 | 0.08 |
| 60~70 | 14 | 0.28 |
| 70~80 | m | 0.32 |
| 80~90 | 6 | 0.12 |
| 90~100 | 10 | 0.20 |
| 合 计 | 1.00 |
(1)学生心理健康测试成绩频率统计表中的m=16;
(2)请补全学生心理健康测试成绩频数统计图;
(3)若成绩在60分以下(不含60分)心理健康状况为不良,60分-70分(含60分)为一般,70分-90分(含70分)为良好,90分(含90分)以上为优秀,请补全学生心理健康状况扇形统计图.

13. 如图是一个正方体,则它的表面展开图可以是( )
如图是一个正方体,则它的表面展开图可以是( )
 如图是一个正方体,则它的表面展开图可以是( )
如图是一个正方体,则它的表面展开图可以是( )| A. |  | B. |  | C. |  | D. |  |
3.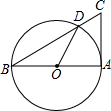 如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )
如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )
 如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )
如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )| A. | 70° | B. | 35° | C. | 20° | D. | 40° |
 甲、乙两车分别从A、B两地沿同一路线同时出发,相向而行,以各自速度匀速行驶,甲车行驶到B地停止,乙车行驶到A地停止,甲车比乙车先到达目的地.设甲、乙两车之间的路程为y(km),乙车行驶的时间为x(h),y与x之间的函数图象如图所示.
甲、乙两车分别从A、B两地沿同一路线同时出发,相向而行,以各自速度匀速行驶,甲车行驶到B地停止,乙车行驶到A地停止,甲车比乙车先到达目的地.设甲、乙两车之间的路程为y(km),乙车行驶的时间为x(h),y与x之间的函数图象如图所示.