题目内容
2. 在⊙O中,弦AB=3,将AB绕点O逆时针旋转60°得弦A′B′,连接OA′,已知OA′⊥AB于C,求⊙O的半径.
在⊙O中,弦AB=3,将AB绕点O逆时针旋转60°得弦A′B′,连接OA′,已知OA′⊥AB于C,求⊙O的半径.
分析 首先连接OA,由旋转的性质,可得∠AOA′=60°,又由OA′⊥AB,根据垂径定理即可求得AC的值,继而求得答案.
解答  解:连接OA,
解:连接OA,
∵将AB绕点O逆时针旋转60°得弦A′B′,
∴∠AOA′=60°,
∵OA′⊥AB,
∴AC=$\frac{1}{2}$AB=$\frac{3}{2}$,
∴OA=$\frac{AC}{sin60°}$=$\sqrt{3}$,
∴⊙O的半径为:$\sqrt{3}$.
点评 此题考查了旋转的性质、垂径定理以及锐角三角函数的知识.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
3.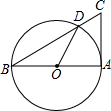 如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )
如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )
 如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )
如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )| A. | 70° | B. | 35° | C. | 20° | D. | 40° |
14.计算:($\frac{21}{26}$)3×($\frac{13}{14}$)4×($\frac{4}{3}$)5=( )
| A. | $\frac{13}{33}$ | B. | $\frac{104}{63}$ | C. | $\frac{2×13}{3×7}$ | D. | $\frac{23×13}{32×7}$ |
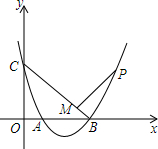 如图,抛物线y=x2-3x+2与坐标轴交于A、B、C三点,点P为抛物线上一点,PM⊥BC于M,且$\frac{PM}{CM}$=$\frac{1}{2}$,求点P的坐标.
如图,抛物线y=x2-3x+2与坐标轴交于A、B、C三点,点P为抛物线上一点,PM⊥BC于M,且$\frac{PM}{CM}$=$\frac{1}{2}$,求点P的坐标. 如图,点P在函数y=$\frac{\sqrt{3}}{x}$(x>0)的图象上运动,O为坐标原点,点A为PO的中点,以点P为圆心,PA为半径作⊙P,则当⊙P与坐标轴相切时,点P的坐标为($\sqrt{3}$,1)或(1,$\sqrt{3}$).
如图,点P在函数y=$\frac{\sqrt{3}}{x}$(x>0)的图象上运动,O为坐标原点,点A为PO的中点,以点P为圆心,PA为半径作⊙P,则当⊙P与坐标轴相切时,点P的坐标为($\sqrt{3}$,1)或(1,$\sqrt{3}$).