题目内容
5.已知$\frac{1}{a}-\frac{1}{b}=\frac{2}{a+b}$,则$\frac{b}{a}+\frac{a}{b}$的值为±2$\sqrt{2}$.分析 先通分,再变形求出$\frac{b}{a}$-$\frac{a}{b}$=2,根据完全平方公式得出($\frac{b}{a}$+$\frac{a}{b}$)2=($\frac{b}{a}$-$\frac{a}{b}$)2+4=8,求出即可.
解答 解:$\frac{1}{a}-\frac{1}{b}=\frac{2}{a+b}$,
$\frac{b-a}{ab}$=$\frac{2}{a+b}$,
$\frac{{b}^{2}-{a}^{2}}{ab}$=2,
∴$\frac{b}{a}$-$\frac{a}{b}$=2,
∴($\frac{b}{a}$+$\frac{a}{b}$)2=($\frac{b}{a}$-$\frac{a}{b}$)2+4=22+4=8,
∴$\frac{b}{a}$+$\frac{a}{b}$=±2$\sqrt{2}$,
故答案为:±2$\sqrt{2}$.
点评 本题考查了分式的混合运算和求值,完全平方公式等知识点,能求出$\frac{b}{a}$-$\frac{a}{b}$=2是解此题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
16.介于$\sqrt{3}$+1和$\sqrt{12}$之间的整数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
13.已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0)、(x2,0),且1<x2<2,与y轴正半轴的交点在(0,2)下方,在下列结论中:①b<0,②4a-2b+c=0,③2a-b+1<0,④b<a<c.其中正确结论是( )
| A. | ①② | B. | ③④ | C. | ①②③ | D. | ①②④ |
8.下列说法:
①若|-a|+a=0,则a≤0;
②两个有理数的和必定大于其中一个加数;
③互为相反数的两个数相乘所得的积是负数;
④立方根等于本身的数是0、1.
其中说法正确的有( )个.
①若|-a|+a=0,则a≤0;
②两个有理数的和必定大于其中一个加数;
③互为相反数的两个数相乘所得的积是负数;
④立方根等于本身的数是0、1.
其中说法正确的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.三角形的一个内角等于其余两个内角的和,则这个三角形是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 钝角三角形 | D. | 锐角三角形 |
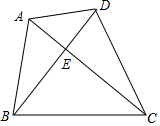 如图,在四边形ABCD中,对角线AC与BD相交于点E,且∠CAB=∠CBD,已知AB=4,AC=6,BC=5,BD=5.5,则DE的长为$\frac{13}{6}$.
如图,在四边形ABCD中,对角线AC与BD相交于点E,且∠CAB=∠CBD,已知AB=4,AC=6,BC=5,BD=5.5,则DE的长为$\frac{13}{6}$.