题目内容

20．解分式方程：
（1）$\frac{1}{x-2}$+3=$\frac{1-x}{2-x}$；
（2）$\frac{x}{x-2}$+$\frac{2}{{x}^{2}-4}$=1．

分析 两分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

解答 解：（1）去分母得：1+3x-6=x-1，
解得：x=2，
经检验x=2是增根，分式方程无解；
（2）去分母得：x2+2x+2=x2-4，
解得：x=-3，
经检验x=-3是分式方程的解．

点评 此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．

练习册系列答案
相关题目
10．使分式$\frac{2}{{x}^{2}-4}$有意义的x取值范围是（　　）
A．x≠2B．x≠-2C．x≠2且x≠-2D．x≠2或x≠-2
11．雾霾天气严重影响市民的生活质量，因此，空气质量备受人们关注，甲城某空气质量监测站点检测了该区域每天的空气质量情况，统计了2015年2月-5月份若干天的情况，并制订了如下两幅不完整的统计图，请根据图中信息，解答下列问题：
（1）统计图共统计了120天空气质量的情况．
（2）请将图中所缺部分补充完整，并计算空气质量为优的所在扇形的圆心角的度数？
（3）计算轻度污染的所占比例，并以此估计2016年2-5月份中大约有多少天受轻度污染？（最后结果用收尾法）
8．【问题背景】
（1）如图1的图形我们把它称为“8字形”，请说明∠A+∠B=∠C+∠D；
【简单应用】
（2）阅读下面的内容，并解决后面的问题：如图2，AP、CP分别平分∠BAD．∠BCD，若∠ABC=36°，∠ADC=16°，求∠P的度数；
解：∵AP、CP分别平分∠BAD．∠BCD
∴∠1=∠2，∠3=∠4
由（1）的结论得：$\left\{\begin{array}{l}{∠P+∠3=∠1+∠B①}\\{∠P+∠2=∠4+∠D②}\end{array}\right.$
①+②，得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P=$\frac{1}{2}$（∠B+∠D）=26°．
【问题探究】如图3，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，若∠ABC=36°，∠ADC=16°，请猜想∠P的度数，并说明理由．

【拓展延伸】
①在图4中，若设∠C=α，∠B=β，∠CAP=$\frac{1}{3}$∠CAB，∠CDP=$\frac{1}{3}$∠CDB，试问∠P与∠C、∠B之间的数量关系为：?∠P=$\frac{2}{3}$α+$\frac{1}{3}$β（用α、β表示∠P），
②在图5中，AP平分∠BAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的关系，直接写出结论∠P=$\frac{180°+∠B+∠D}{2}$．
15．如今，留守儿童的监护问题已成为社会关注的焦点．我省相关部门就某县儿童监护情况进行了调查，将调查出现的情况分四类，即A类：委托他人监护或父母监护能力缺失；B类：隔代监护；C类：父母一方在家监护；D类：父母双方在家监护．通过调查，得到下面两幅不完整的统计图，请根据图中的信息解决下面的问题．
（1）在这次随机抽样调查中，共抽查了多少名学生儿童？
（2）这次调查中B类儿童有30人；扇形统计图中D类儿童数所占的圆心角是72度．
（3）根据最新的文件精神，符合A、B两种类型的儿童被定义为留守儿童，请你估计该县50000名儿童中，留守儿童有多少人？
5．已知$\frac{1}{a}-\frac{1}{b}=\frac{2}{a+b}$，则$\frac{b}{a}+\frac{a}{b}$的值为±2$\sqrt{2}$．
6．不等式（2-$\sqrt{5}$）x＞1的解集是x＜-2-$\sqrt{5}$．
3．已知一个等腰三角形两内角的度数之比为1：4，则这个等腰三角形的底角的度数为（　　）
A．30°B．30°或120°C．80°D．30°或80°
4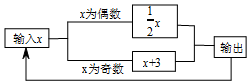．如图所示的运算程序中，若开始输入的x值为96，我们发现第一次输出的结果为48，第二次输出的结果为24，…，则第2014次输出的结果为（　　）
A．6B．3C．$\frac{3}{{2}^{2007}}$D．6024

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网