题目内容
11.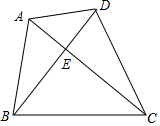 如图,在四边形ABCD中,对角线AC与BD相交于点E,且∠CAB=∠CBD,已知AB=4,AC=6,BC=5,BD=5.5,则DE的长为$\frac{13}{6}$.
如图,在四边形ABCD中,对角线AC与BD相交于点E,且∠CAB=∠CBD,已知AB=4,AC=6,BC=5,BD=5.5,则DE的长为$\frac{13}{6}$.
分析 直接利用相似三角形的判定方法得出△ABC∽△BEC,进而利用相似三角形的性质得出答案.
解答 解:∵∠CAB=∠CBD,∠ACB=∠BCE,
∴△ABC∽△BEC,
∴$\frac{AB}{BE}$=$\frac{AC}{BC}$,
∵AB=4,AC=6,BC=5,BD=5.5,
∴$\frac{4}{5.5-DE}$=$\frac{6}{5}$,
解得:DE=$\frac{13}{6}$.
故答案为:$\frac{13}{6}$.
点评 此题主要考查了相似三角形的判定与性质,正确得出△ABC∽△BEC是解题关键.

练习册系列答案
相关题目
3.已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形的底角的度数为( )
| A. | 30° | B. | 30°或120° | C. | 80° | D. | 30°或80° |
20.下列四组有理数大小的比较正确的是( )
| A. | -$\frac{1}{2}$>-$\frac{1}{3}$ | B. | -(-1)>|-1| | C. | $\frac{1}{2}$<-$\frac{1}{3}$ | D. | |-$\frac{1}{2}$|>|-$\frac{1}{3}$| |
1. 如图,AB∥CD,CE平分∠BCD,∠DCE=20°,则∠B的度数为( )
如图,AB∥CD,CE平分∠BCD,∠DCE=20°,则∠B的度数为( )
 如图,AB∥CD,CE平分∠BCD,∠DCE=20°,则∠B的度数为( )
如图,AB∥CD,CE平分∠BCD,∠DCE=20°,则∠B的度数为( )| A. | 18° | B. | 40° | C. | 45° | D. | 54° |
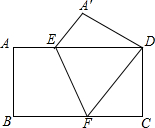 如图:把一个矩形如图折叠,使顶点B和D重合,折痕为EF.
如图:把一个矩形如图折叠,使顶点B和D重合,折痕为EF.
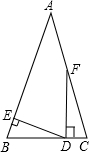 如图,已知△ABC中,∠B=∠C,D是边BC上一点,DE⊥AB,垂足为点E,DF⊥BC,DF交边AC于点F,∠AFD=155°,则∠EDF=65°.
如图,已知△ABC中,∠B=∠C,D是边BC上一点,DE⊥AB,垂足为点E,DF⊥BC,DF交边AC于点F,∠AFD=155°,则∠EDF=65°.